题目内容
(本小题满分14分)设数列 满足
满足 且对一切
且对一切 ,有
,有 .
.
(1)求 的值;
的值;
(2)证明:数列 为等差数列;
为等差数列;
(3)求数列 的通项公式;
的通项公式;
(4)设 ,求证:
,求证: .
.
(1) (2)见解析;(3)
(2)见解析;(3) ;(4)见解析
;(4)见解析
【解析】
试题分析:(1)令 代入
代入 (2)利用
(2)利用 构造
构造 (3)因为数列
(3)因为数列 为等差数列,所以能求出
为等差数列,所以能求出 ,再利用迭加法求出
,再利用迭加法求出 ;(4)先求出
;(4)先求出 ,利用裂项相消求出
,利用裂项相消求出
试题解析:(1) 2分
2分
(2)由 可得:
可得:

∴数列 为等差数列,且首项
为等差数列,且首项  ,公差为
,公差为 6分
6分
(3)∴ 8分
8分
∴ 10分
10分
(4)由(2)可知:
 12分
12分
∴

 14分
14分

考点:等差数列的证明,迭加法求通项,数列求和裂项相消

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 中,
中, ,则
,则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 上一点M到焦点的距离是
上一点M到焦点的距离是 ,则点M的横坐标是( )
,则点M的横坐标是( ) B.
B. C.
C. D.
D.
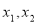
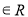 ,常数
,常数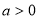 ,定义运算“*”:
,定义运算“*”: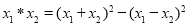 ,若
,若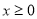 ,则动点P(
,则动点P(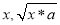 )的轨迹是( )
)的轨迹是( ) 有公共渐近线的双曲线方程为( )
有公共渐近线的双曲线方程为( )



 是定义在
是定义在 上的偶函数,且在
上的偶函数,且在 上是增函数,设
上是增函数,设 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( ) B.
B. C.
C. D.
D.
 ,则该三棱锥外接球的表面积为____.
,则该三棱锥外接球的表面积为____.