题目内容
设x≥1，y≥1，证明x＋y＋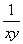
≤
＋
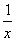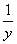＋xy；
)由于x≥1，y≥1，所以
x＋y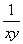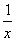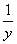＋≤＋＋xy⇔xy(x＋y)＋1≤y＋x＋(xy)2.
将上式中的右式减左式，得
[y＋x＋(xy)2]－[xy(x＋y)＋1]＝[(xy)2－1]－[xy(x＋y)－(x＋y)]＝(xy＋1)(xy－1)－(x＋y)(xy－1)＝(xy－1)(xy－x－y＋1)＝(xy－1)(x－1)(y－1)．
既然x≥1，y≥1，所以(xy－1)(x－1)(y－1)≥0，从而所要证明的不等式成立
练习册系列答案
相关题目
若x，y为整数，则3x＋4y的最小值是( )．
＋
，B＝
＋
＜α＜β＜
，集合∁UA＝{y|y＝x
，
则不等式f(x)≤2的解集是________．
的三内角
、
、
所对边的边长分别为
、
、
，且 
，
, 则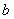
的取值范围为………（ ）.
． 
．
． 
．