题目内容
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为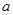 、
、 、
、 ,且满足
,且满足

 。
。
(1)求角 的大小;
的大小;
(2)若 ,
, ,试判断
,试判断 的形状,并说明理由
的形状,并说明理由
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为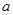 、
、 、
、 ,且满足
,且满足

 。
。(1)求角
 的大小;
的大小;(2)若
 ,
, ,试判断
,试判断 的形状,并说明理由
的形状,并说明理由 (1) (2)等边三角形
(2)等边三角形
 (2)等边三角形
(2)等边三角形本试题主要考查了解三角形的运用。
解:(1)法一:∵(2b-c)cosA-acosC=0,
由正弦定理得,(2sinB-sinC)cosA-sinAcosC=0,
∴2sinBcosA-sin(A+C)=0,即sinB(2cosA-1)=0.∵0<B<π,∴sinB≠0,∴cosA=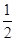 .
.
∵0<A<π,∴A= .
.
法二:∵(2b-c)cosA-acosC=0,由余弦定理得,(2b-c)·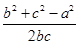 -a·
-a·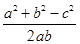 =0,整理得b2+c2-a2=bc,∴cosA=
=0,整理得b2+c2-a2=bc,∴cosA=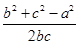 =
=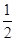 .∵0<A<π,∴A=
.∵0<A<π,∴A= .
.
(2)∵S△ABC=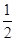 bcsinA=
bcsinA=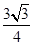 ,即bcsin
,即bcsin =
=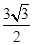 ,
,
∴bc=3,①∵a2=b2+c2-2bccosA,∴b2+c2=6,②
由①②得b=c=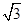 ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.
解:(1)法一:∵(2b-c)cosA-acosC=0,
由正弦定理得,(2sinB-sinC)cosA-sinAcosC=0,
∴2sinBcosA-sin(A+C)=0,即sinB(2cosA-1)=0.∵0<B<π,∴sinB≠0,∴cosA=
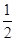 .
.∵0<A<π,∴A=
 .
.法二:∵(2b-c)cosA-acosC=0,由余弦定理得,(2b-c)·
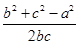 -a·
-a·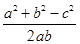 =0,整理得b2+c2-a2=bc,∴cosA=
=0,整理得b2+c2-a2=bc,∴cosA=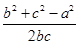 =
=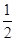 .∵0<A<π,∴A=
.∵0<A<π,∴A= .
.(2)∵S△ABC=
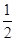 bcsinA=
bcsinA=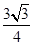 ,即bcsin
,即bcsin =
=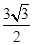 ,
,∴bc=3,①∵a2=b2+c2-2bccosA,∴b2+c2=6,②
由①②得b=c=
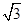 ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.
练习册系列答案
相关题目
 中,
中, ,且最大边长和最小边长是方程
,且最大边长和最小边长是方程 的两个根,则第三边的长为( )
的两个根,则第三边的长为( )



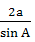 -
-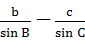 = ______________
= ______________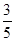 ,则底边上的高与底边的比值为
,则底边上的高与底边的比值为


 中,若
中,若 ,则
,则 为锐角,
为锐角, ,
, ,则
,则 的值为( )
的值为( )
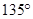

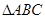 中,角
中,角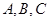 所对的边分别为
所对的边分别为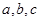 ,若
,若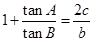 ,则角
,则角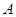 的大小为_________.
的大小为_________.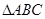 中,
中,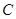 为钝角,
为钝角, ,
,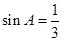 ,则角
,则角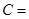 _______,
_______,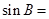 ______.
______. 中,三边
中,三边 、
、 、
、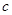 所对的角分别为
所对的角分别为 、
、 、
、 ,已知
,已知 ,
, ,
, ,则sin
,则sin