题目内容
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() :
:![]() 上的点按坐标变换
上的点按坐标变换![]() ,得到曲线
,得到曲线![]() ,
,![]() 为
为![]() 与
与![]() 轴负半轴的交点,经过点
轴负半轴的交点,经过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,与曲线
,与曲线![]() 的交点分别为
的交点分别为![]() ,
,![]() (点
(点![]() 在第二象限).
在第二象限).
(Ⅰ)写出曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(Ⅱ)求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,
,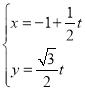 (
(![]() 为参数);(Ⅱ)
为参数);(Ⅱ)![]()
【解析】
(Ⅰ)利用伸缩变换公式,把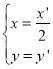 代入
代入![]() 的方程
的方程![]() ,化简整理即可;由曲线
,化简整理即可;由曲线![]() 的方程求出点
的方程求出点![]() 的坐标,利用倾斜角求出其余弦值和正弦值,代入直线参数方程的标准形式即可求解;
的坐标,利用倾斜角求出其余弦值和正弦值,代入直线参数方程的标准形式即可求解;
(Ⅱ)利用弦长公式求出![]() ,联立直线的参数方程和曲线
,联立直线的参数方程和曲线![]() 的方程,利用直线参数方程中参数
的方程,利用直线参数方程中参数![]() 的几何意义求出
的几何意义求出![]() ,进而求出
,进而求出![]() 的值.
的值.
(Ⅰ)由题得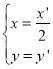 代入
代入![]() 的方程
的方程![]() 得
得
![]() :
:![]() ,即
,即![]() 的方程为
的方程为![]() ,
,
因为曲线![]() :
:![]() ,令
,令![]() ,则
,则![]() ,
,
因为![]() 为
为![]() 与
与![]() 轴负半轴的交点,所以点
轴负半轴的交点,所以点![]() ,
,
因为直线![]() 的倾斜角为
的倾斜角为![]() ,所以
,所以![]() ,
,
所以![]() 的参数方程为
的参数方程为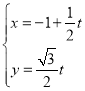 (
(![]() 为参数);
为参数);
(Ⅱ)因为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
因为圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,所以圆心
,所以圆心![]() 到直线
到直线![]() 的距离为
的距离为
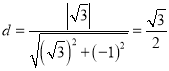 ,
,
由弦长公式可得,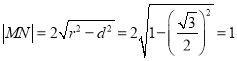 ,
,
将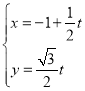 (
(![]() 为参数)代入
为参数)代入![]() ,整理得
,整理得![]() ,
,
设![]() ,
,![]() 为方程的两个根,则
为方程的两个根,则![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




