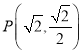题目内容
【题目】
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(I)![]() (II)存在点
(II)存在点![]() 使得
使得![]() 与
与![]() 的面积相等,此时点
的面积相等,此时点![]() 的坐标为
的坐标为![]() .
.
【解析】
试题(1)利用直接法设![]() ,利用直线
,利用直线![]() 与
与![]() 的斜率之积等于
的斜率之积等于![]() ,得到关于
,得到关于![]() 的方程,求得其轨迹方程;(2)根据题意设
的方程,求得其轨迹方程;(2)根据题意设![]()
![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() 三个点的坐标,再利用三角形的面积公式和点到直线的距离公式,求得
三个点的坐标,再利用三角形的面积公式和点到直线的距离公式,求得![]() 和
和![]() 的面积,利用
的面积,利用![]()
![]() ,进而得到关于
,进而得到关于![]() 的方程,求得点
的方程,求得点![]() 的坐标为
的坐标为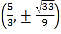 .
.
试题解析:(1)点![]() 的轨迹方程为
的轨迹方程为![]() ; 5分
; 5分
(2)设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,
,
于是![]() 的面积
的面积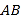 , 8分
, 8分
直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
于是![]() 的面积
的面积![]()
![]() , 10分
, 10分
当![]()
![]() 时,得
时,得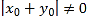 ,
,
又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故存在点![]() 使得
使得![]() 与
与![]() 的面积相等,
的面积相等,
此时点![]() 的坐标为
的坐标为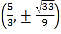 . 12分
. 12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.