题目内容
点P是球O的直径AB上的动点,PA=x,过点P且与AB垂直的截面面积记为f(x),则y=
f(x)的大致图象是
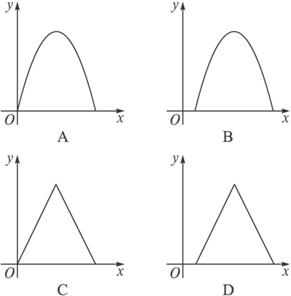
A 设截面圆的半径为r,则r2=x(2R-x).∴f(x)=πr2=π·x(2R-x).
∴y=
f(x)=-
(x-R)2+.其图象是过原点且开口向下的抛物线的一部分.故选A.
练习册系列答案
相关题目
f(x)的大致图象是题目内容
点P是球O的直径AB上的动点,PA=x,过点P且与AB垂直的截面面积记为f(x),则y=f(x)的大致图象是
A 设截面圆的半径为r,则r2=x(2R-x).∴f(x)=πr2=π·x(2R-x).
∴y=f(x)=-(x-R)2+.其图象是过原点且开口向下的抛物线的一部分.故选A.
，过P点且与直径AB垂直的截面积记为
（如图所示），则函数
的图象大致是（ ）
，过点
且与AB垂直的截面面积记为y，则
的图像是（ ）