题目内容
【题目】祖暅是南北朝时代的伟大科学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等．现有以下四个几何体：图①是从圆柱中挖出一个圆锥所得的几何体；图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为（ ）
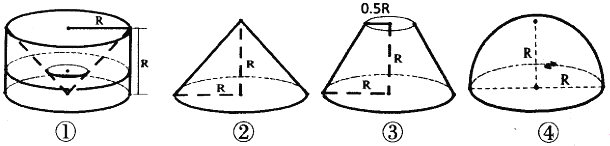
A. ①② B. ①③ C. ②④ D. ①④
【答案】D
【解析】设截面与底面的距离为
，则①中截面内圆半径为
，则截面圆环的面积为
；②中截面圆的半径为
，则截面圆的面积为
；③中截面圆的半径为
，则截面圆的面积为
；②中截面圆的半径为
，则截面圆的面积为
，所以①④中截面的面积相等，故选D．
练习册系列答案
一线名师权威作业本系列答案
相关题目
【题目】已知f（x）=max{x2﹣ax+a，ax﹣a+1}，其中max{x，y}= 
． （Ⅰ）若对任意x∈R，恒有f（x）=x2﹣ax+a，求实数a的值；
（Ⅱ）若a＞1，求f（x）的最小值m（a）．
