题目内容
设函数f(x)=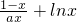 在[1,+∞)上为增函数.
在[1,+∞)上为增函数.
(1)求正实数a的取值范围;
(2)若a=1,求证: (n∈N*且n≥2).
(n∈N*且n≥2).
解:(1)由已知:f'(x)= .
.
依题意得: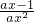 ≥0对x∈[1,+∞)恒成立.
≥0对x∈[1,+∞)恒成立.
∴ax-1≥0对x∈[1,+∞)恒成立,∴a-1≥0,即:a≥1.
故正实数a的取值范围为[1,+∞).
(2)∵a=1,∴由(1)知:f(x)= 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,
∴n≥2时:f( )=
)= ,
,
即: …. (9分)
…. (9分)
∴ .
.
设g(x)=lnx-x,x∈[1,+∞),则 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,
∴g′(x)在[1+∞)为减函数.
∴n≥2时:g( )=ln
)=ln -
- <g(1)=-1<0,
<g(1)=-1<0,
即:ln <
< =1+
=1+ (n≥2).
(n≥2).
∴lnn= ,
,
综上所证: (n∈N*且≥2)成立.
(n∈N*且≥2)成立.
分析:(1)由已知可得f'(x)=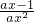 ≥0对x∈[1,+∞)恒成立,即ax-1≥0对x∈[1,+∞)恒成立,可得a-1≥0,从而
≥0对x∈[1,+∞)恒成立,即ax-1≥0对x∈[1,+∞)恒成立,可得a-1≥0,从而
求得正实数a的取值范围.
(2)根据n≥2时:f( )>f(1)=0,可得
)>f(1)=0,可得 ,从而得到
,从而得到  <lnn;设g(x)=
<lnn;设g(x)=
lnx-x,x∈[1,+∞),则 对x∈[1,+∞)恒成立,故 n≥2时,由g(
对x∈[1,+∞)恒成立,故 n≥2时,由g( )<g(1)=-1<0,得
)<g(1)=-1<0,得
ln <1+
<1+ ,由此利用放缩法证得lnn<
,由此利用放缩法证得lnn< ,从而证得不等式成立.
,从而证得不等式成立.
点评:本题主要考查利用导数研究函数的单调性,用放缩法证明不等式,将式子进行恰当的放缩,是解题的难点.
 .
.依题意得:
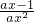 ≥0对x∈[1,+∞)恒成立.
≥0对x∈[1,+∞)恒成立.∴ax-1≥0对x∈[1,+∞)恒成立,∴a-1≥0,即:a≥1.
故正实数a的取值范围为[1,+∞).
(2)∵a=1,∴由(1)知:f(x)=
 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,∴n≥2时:f(
 )=
)= ,
,即:
 …. (9分)
…. (9分)∴
 .
.设g(x)=lnx-x,x∈[1,+∞),则
 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,∴g′(x)在[1+∞)为减函数.
∴n≥2时:g(
 )=ln
)=ln -
- <g(1)=-1<0,
<g(1)=-1<0,即:ln
 <
< =1+
=1+ (n≥2).
(n≥2).∴lnn=
 ,
,综上所证:
 (n∈N*且≥2)成立.
(n∈N*且≥2)成立.分析:(1)由已知可得f'(x)=
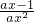 ≥0对x∈[1,+∞)恒成立,即ax-1≥0对x∈[1,+∞)恒成立,可得a-1≥0,从而
≥0对x∈[1,+∞)恒成立,即ax-1≥0对x∈[1,+∞)恒成立,可得a-1≥0,从而求得正实数a的取值范围.
(2)根据n≥2时:f(
 )>f(1)=0,可得
)>f(1)=0,可得 ,从而得到
,从而得到  <lnn;设g(x)=
<lnn;设g(x)=lnx-x,x∈[1,+∞),则
 对x∈[1,+∞)恒成立,故 n≥2时,由g(
对x∈[1,+∞)恒成立,故 n≥2时,由g( )<g(1)=-1<0,得
)<g(1)=-1<0,得ln
 <1+
<1+ ,由此利用放缩法证得lnn<
,由此利用放缩法证得lnn< ,从而证得不等式成立.
,从而证得不等式成立.点评:本题主要考查利用导数研究函数的单调性,用放缩法证明不等式,将式子进行恰当的放缩,是解题的难点.

练习册系列答案
相关题目