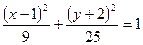题目内容
(本小题共14分)
已知椭圆的中心在原点,焦点在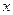 轴上,经过点
轴上,经过点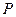
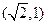 且离心率
且离心率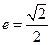 .过定点
.过定点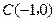 的直线与椭圆相交于
的直线与椭圆相交于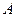 ,
,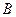 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)在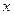 轴上是否存在点
轴上是否存在点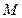 ,使
,使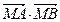 为常数?若存在,求出点
为常数?若存在,求出点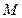 的坐标;若不存
的坐标;若不存
在,请说明理由.
已知椭圆的中心在原点,焦点在
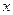 轴上,经过点
轴上,经过点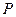
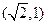 且离心率
且离心率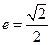 .过定点
.过定点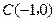 的直线与椭圆相交于
的直线与椭圆相交于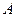 ,
,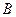 两点.
两点.(Ⅰ)求椭圆的方程;
(Ⅱ)在
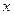 轴上是否存在点
轴上是否存在点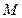 ,使
,使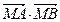 为常数?若存在,求出点
为常数?若存在,求出点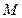 的坐标;若不存
的坐标;若不存在,请说明理由.
(Ⅰ)设椭圆方程为
由已知可得 ,解得
,解得  .
.
所求椭圆的方程为 . -------------5分
. -------------5分
(Ⅱ)设
当直线 与
与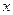 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 .
.

 ,
, ,
,


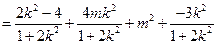

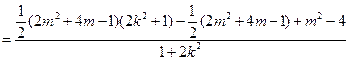
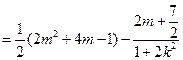
 是与
是与 无关的常数,
无关的常数,
∴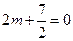
∴ ,即
,即 .
.
此时, .
.
当直线 与
与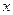 轴垂直时,则直线
轴垂直时,则直线 的方程为
的方程为 .
.
此时点 的坐标分别为
的坐标分别为
当 时, 亦有
时, 亦有
综上,在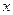 轴上存在定点
轴上存在定点 ,使
,使 为常数.------------ 14分
为常数.------------ 14分

由已知可得
 ,解得
,解得  .
.所求椭圆的方程为
 . -------------5分
. -------------5分(Ⅱ)设

当直线
 与
与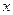 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 .
.
 ,
, ,
,

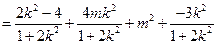

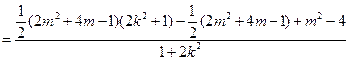
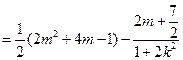
 是与
是与 无关的常数,
无关的常数,∴
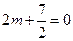
∴
 ,即
,即 .
.此时,
 .
.当直线
 与
与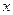 轴垂直时,则直线
轴垂直时,则直线 的方程为
的方程为 .
.此时点
 的坐标分别为
的坐标分别为
当
 时, 亦有
时, 亦有
综上,在
 轴上存在定点
轴上存在定点 ,使
,使 为常数.------------ 14分
为常数.------------ 14分略

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
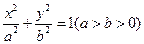 的左、右焦点分别为
的左、右焦点分别为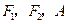 是椭圆上的一点,
是椭圆上的一点,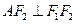 ,原点
,原点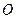 到直线
到直线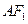 的距离为
的距离为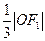 .
.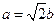 ;
;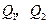 为椭圆上的两个动点,
为椭圆上的两个动点,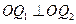 ,过原点
,过原点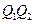 的垂线
的垂线 ,垂足为
,垂足为 ,求点
,求点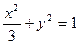 上的一个动点,求S=x+y的最大值。
上的一个动点,求S=x+y的最大值。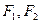 的坐标分别为
的坐标分别为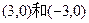
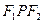 的面积
的面积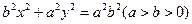 的左焦点F。右顶点A,上顶点B,若
的左焦点F。右顶点A,上顶点B,若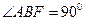 ,则椭圆的离心率是( )
,则椭圆的离心率是( )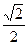
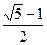
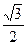
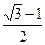
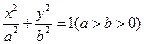 的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且
的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且 是边长为2的正三角形;又椭圆E上的P、Q两点关于直线
是边长为2的正三角形;又椭圆E上的P、Q两点关于直线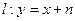 对称.
对称.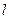 过点(
过点(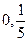 )时,求直线PQ的方程;
)时,求直线PQ的方程;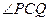 =
=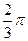 ,求
,求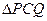 面积的最大值.
面积的最大值.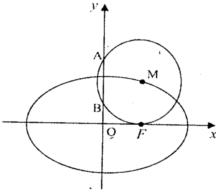


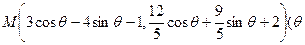 为参数)的轨迹的普通方程为( )
为参数)的轨迹的普通方程为( )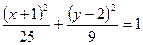 B
B 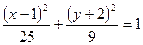
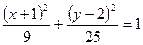 D
D