题目内容
已知椭圆
过点D（1，
），焦点为
，满足
.
(Ⅰ)求椭圆C的方程；
（Ⅱ）若过点（2，0）的直线与椭圆C相交于两点A、B，P为椭圆上一点，且满足
(其中O为坐标原点)，求整数t的最大值.
解：（Ⅰ）解析：由已知过点
,得
，①
记c＝
，不妨设F1(－c，0)，F2(c，0)，则
＝(－c－1，－
)，
＝(c－1，－)，
由
，得c2＝1，即a2－b2＝1．②
由①、②，得
，b2＝1．
故椭圆
的方程为
．……………………………………………… 5分
（Ⅱ）由题意知，直线
的斜率存在.
设：
，
，
，
，
由
得
.
，
.
，
，…………………………………………………8分
∵
，∴
，
，
.
∵点
在椭圆上，∴
，
∴
，…………………………………………………………………12分
，∴
的最大整数值为1. ………13分
练习册系列答案
相关题目
过点(0，1)，且离心率为
．
与x轴交于点D，点P是椭圆C上异于A，B的动点，直线AP，BP分别交直线l于E，F两点．证明：当点P在椭圆C上运动时，|DE|·|DF|恒为定值．
过点(0，1)，且离心率为
．
与x轴交于点D，点P是椭圆C上异于A1，A2的动点，直线A1P，A2P分别交直线l于E，F两点．证明：|DE|·|DF|恒为定值．
，－4)和点Q(－
，3)，则此椭圆的标准方程是 
+x2=1 B.
+y2=1
+y2=1或x2+
=1 D.以上都不对
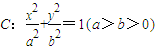过点D（1，
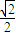），焦点为F1，F2，满足
．
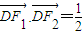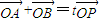（其中O为坐标原点），求整数t的最大值．