题目内容
设 (
( 是正整数),利用赋值法解决下列问题:
是正整数),利用赋值法解决下列问题:
(1)求 ;
;
(2) 为偶数时,求
为偶数时,求 ;
;
(3) 是3的倍数时,求
是3的倍数时,求 。
。
(1)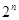 ;(2)
;(2) 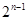 ;(3)
;(3)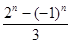 。
。
解析试题分析:(1)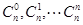 为二项式
为二项式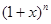 展开式中每一项的二项式系数,令
展开式中每一项的二项式系数,令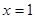 可求得
可求得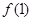 ,即
,即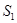 的值,(2)
的值,(2)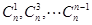 为
为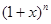 的展开式中偶数项的二项式系数,令
的展开式中偶数项的二项式系数,令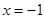 可得
可得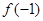 的值,再与
的值,再与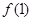 相加即可得
相加即可得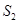 ,(3)利用复数
,(3)利用复数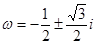 次方的性质,构造方程,从而求得
次方的性质,构造方程,从而求得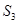 的值。
的值。
试题解析:令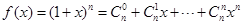 ,
,
(1)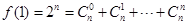 ,所以
,所以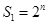
(2)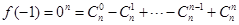 ,
,
所以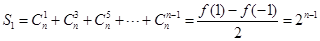
(3)记 ,则
,则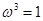 。当
。当 时,
时,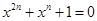 ,当
,当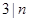 时,
时, ,
,
记 ,
,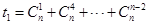 ,
,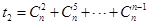
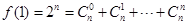 ,
,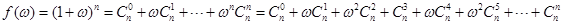 ,
,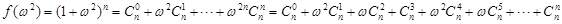 ,
,
则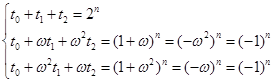
从上到下各式分别乘以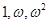 ,求得
,求得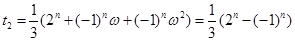 。即
。即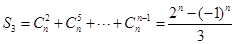
考点:(1)赋值法的应用;(2)复数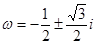 性质的应用。
性质的应用。

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
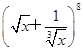 的展开式中二项式系数最大项.
的展开式中二项式系数最大项. 展开式的二项式系数之和为256.
展开式的二项式系数之和为256. ;
; ,求
,求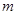 的值;
的值; 展开式中系数最大项只有第6项和第7项,求
展开式中系数最大项只有第6项和第7项,求 -
-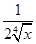 )n的展开式中,前三项系数的绝对值依次成等差数列.
)n的展开式中,前三项系数的绝对值依次成等差数列.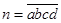 的各位数码
的各位数码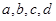 中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义
中,任三个数码皆可构成一个三角形的三条边长,则称为四位三角形数,定义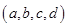 为的数码组,其中
为的数码组,其中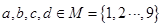 若 数码组为
若 数码组为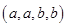 型,
型,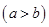 , 试求所有四位三角形数的个数.
, 试求所有四位三角形数的个数.  的展开式中的常数项是__________.
的展开式中的常数项是__________.