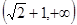题目内容
讨论方程 (
( )所表示的曲线类型.
)所表示的曲线类型.
 (
( )所表示的曲线类型.
)所表示的曲线类型.当 时,此方程表示焦点在
时,此方程表示焦点在 轴上的双曲线;当
轴上的双曲线;当 时,此方程表示焦点在
时,此方程表示焦点在 轴上的椭圆.
轴上的椭圆.
 时,此方程表示焦点在
时,此方程表示焦点在 轴上的双曲线;当
轴上的双曲线;当 时,此方程表示焦点在
时,此方程表示焦点在 轴上的椭圆.
轴上的椭圆.试题分析:当
 时,此方程表示焦点在
时,此方程表示焦点在 轴上的双曲线;
轴上的双曲线;当
 时,此方程表示焦点在
时,此方程表示焦点在 轴上的椭圆.
轴上的椭圆.点评:(1)做此题时,我们要注意讨论的不重不漏。(2)我们熟练掌握判断椭圆、双曲线以及圆的方程的特点。方程
 ,当
,当 且
且 时表示椭圆;(当
时表示椭圆;(当 时,表示焦点在x轴上的椭圆;当
时,表示焦点在x轴上的椭圆;当 时表示焦点在y轴上的椭圆。)当
时表示焦点在y轴上的椭圆。)当 时,表示双曲线;当
时,表示双曲线;当 时,表示圆。
时,表示圆。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
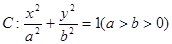 的离心率为
的离心率为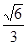 ,
,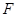 为椭圆的右焦点,
为椭圆的右焦点,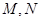 两点在椭圆
两点在椭圆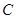 上,且
上,且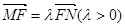 ,定点
,定点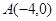 。
。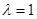 时,有
时,有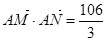 ,求椭圆
,求椭圆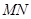 斜率为k,且设
斜率为k,且设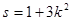 时,试求
时,试求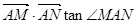 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时 与直线4x+3y + 1 =0相切,动圆M与
与直线4x+3y + 1 =0相切,动圆M与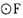 及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向
及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向 各引一条切线,切点 分别为P,Q,记
各引一条切线,切点 分别为P,Q,记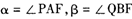 .求证
.求证 是定值.
是定值. 的焦点为
的焦点为 、
、 ,离心率为
,离心率为 ,过点
,过点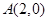 的直线
的直线 交椭圆
交椭圆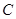 于
于 、
、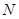 两点.
两点.
 的取值范围;
的取值范围; 和
和 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由. 的两个焦点为
的两个焦点为 ,
, 为坐标原点,点
为坐标原点,点 在双曲线上,且
在双曲线上,且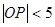 ,若
,若 、
、 、
、 成等比数列,则
成等比数列,则 等于
等于 

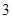

 到点
到点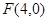 的距离比它到直线
的距离比它到直线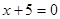 的距离少1,则动点
的距离少1,则动点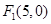 ,
,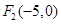 ,曲线上的点P到
,曲线上的点P到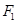 、
、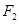 的距离之差的绝对值是6,则该曲线的方程为( )
的距离之差的绝对值是6,则该曲线的方程为( )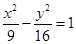
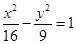
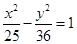
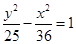
 ,0),则椭圆的标准方程是
,0),则椭圆的标准方程是  分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若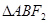 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是