题目内容
(2011•顺义区一模)在△ABC中,a,b,c分别为三个内角A,B,C所对的边,且b2+c2-a2=
bc,则2cosBcosC-cos(B-C)的值为
| 3 |
-
| ||
| 2 |
-
.
| ||
| 2 |
分析:利用余弦定理表示出cosA,将已知的等式代入求出cosA的值,将所求式子第二项利用两角和与差的余弦函数公式化简,去括号合并后再利用两角和与差的余弦函数公式化简,利用诱导公式变形后,将cosA的值代入,即可求出值.
解答:解:∵b2+c2-a2=
bc,
∴cosA=
=
=
,
又A+B+C=π,即B+C=π-A,
则2cosBcosC-cos(B-C)=2cosBcosC-(cosBcosC+sinBsinC)
=cosBcosC-sinBsinC=cos(B+C)=cos(π-A)=-cosA=-
.
故答案为:-
| 3 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| ||
| 2bc |
| ||
| 2 |
又A+B+C=π,即B+C=π-A,
则2cosBcosC-cos(B-C)=2cosBcosC-(cosBcosC+sinBsinC)
=cosBcosC-sinBsinC=cos(B+C)=cos(π-A)=-cosA=-
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:此题考查了余弦定理,两角和与差的余弦函数公式,以及诱导公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
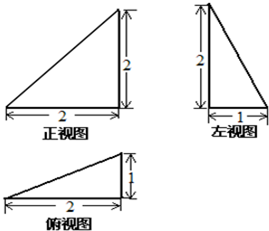 (2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )
(2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )