题目内容
已知椭圆C：
的焦点为F1，F2，若点P在椭圆上，且满足|PO|2=|PF1|•|PF2|（其中为坐标原点），则称点P为“★点”，那么下列结论正确的是
- A.．椭圆上的所有点都是“★点”
- B.．椭圆上仅有有限个点是“★点”
- C.．椭圆上的所有点都不是“★点”
- D.．椭圆上有无穷多个点（但不是所有的点）是“★点”
B
分析：设椭圆上的点P（x0，y0），通过焦半径公式，利用|PO|2=|PF1|•|PF2|，求出x0，得到结果．
解答：设椭圆上的点P（x0，y0），|PF1|=2-ex0，|PF2|=2+ex0，因为|PO|2=|PF1|•|PF2|，则有
，解得
，因此满足条件的有四个点，
故选B．
点评：本题主要考查椭圆的新定义问题，特别是焦半径的转化问题．考查计算能力．
分析：设椭圆上的点P（x0，y0），通过焦半径公式，利用|PO|2=|PF1|•|PF2|，求出x0，得到结果．
解答：设椭圆上的点P（x0，y0），|PF1|=2-ex0，|PF2|=2+ex0，因为|PO|2=|PF1|•|PF2|，则有
，解得，因此满足条件的有四个点，故选B．
点评：本题主要考查椭圆的新定义问题，特别是焦半径的转化问题．考查计算能力．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
的焦点在y轴上，且离心率为
．过点M(0，3)的直线l与椭圆C相交于两点A、B．（1）求椭圆C的方程；（2）设P为椭圆上一点，且满足
（O为坐标原点），当|
|<
时，求实数λ的取值范围．
的焦点在y轴上，且离心率为
．过点M(0，3)的直线l与椭圆C相交于两点A、B． （1）求椭圆C的方程；（2）设P为椭圆上一点，且满足
（O为坐标原点），当|
|<
时，求实数λ的取值范围．
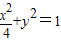的焦点为F1，F2，若点P在椭圆上，且满足|PO|2=|PF1|•|PF2|（其中为坐标原点），则称点P为“★点”，那么下列结论正确的是（ ）
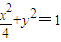的焦点为F1，F2，若点P在椭圆上，且满足|PO|2=|PF1|•|PF2|（其中为坐标原点），则称点P为“★点”，那么下列结论正确的是（ ）