题目内容
已知椭圆 的右顶点A为抛物线y2=8x的焦点,上顶点为B,离心率为
的右顶点A为抛物线y2=8x的焦点,上顶点为B,离心率为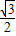
(1)求椭圆C的方程;
(2)过点
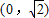 且斜率为k的直线l与椭圆C相交于P,Q两点,若线段PQ的中点横坐标是
且斜率为k的直线l与椭圆C相交于P,Q两点,若线段PQ的中点横坐标是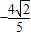 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)利用椭圆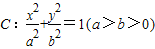 的右顶点A为抛物线y2=8x的焦点,确定a的值,根据离心率,可得椭圆的几何量,从而可得椭圆的标准方程;
的右顶点A为抛物线y2=8x的焦点,确定a的值,根据离心率,可得椭圆的几何量,从而可得椭圆的标准方程;
(2)直线与椭圆方程联立,利用韦达定理,根据线段PQ的中点横坐标是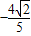 ,即可求得直线l的方程.
,即可求得直线l的方程.
解答: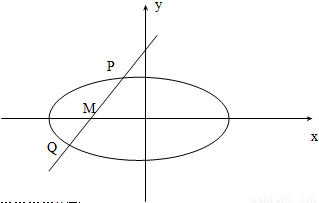 解:(1)抛物线y2=8x的焦点为A(2,0),
解:(1)抛物线y2=8x的焦点为A(2,0),
∵椭圆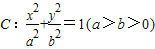 的右顶点A为抛物线y2=8x的焦点
的右顶点A为抛物线y2=8x的焦点
∴a=2…(2分)
∵离心率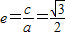 ,∴
,∴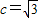 …(3分)
…(3分)
故b2=a2-c2=1…(5分)
所以椭圆C的方程为: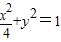 …(6分)
…(6分)
(2)设直线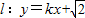
由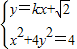 ,消去y可得
,消去y可得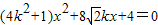 …(8分)
…(8分)
因为直线l与椭圆C相交于P,Q两点,所以△=128k2-16(4k2+1)>0
解得 …(9分)
…(9分)
又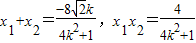 …(10分)
…(10分)
设P(x1,y1),Q(x2,y2),PQ中点M(x,y)
因为线段PQ的中点横坐标是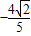 ,所以
,所以 …(12分)
…(12分)
解得k=1或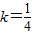 …(13分)
…(13分)
因为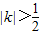 ,所以k=1
,所以k=1
因此所求直线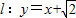 …(14分)
…(14分)
点评:本题考查抛物线的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.
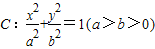 的右顶点A为抛物线y2=8x的焦点,确定a的值,根据离心率,可得椭圆的几何量,从而可得椭圆的标准方程;
的右顶点A为抛物线y2=8x的焦点,确定a的值,根据离心率,可得椭圆的几何量,从而可得椭圆的标准方程;(2)直线与椭圆方程联立,利用韦达定理,根据线段PQ的中点横坐标是
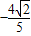 ,即可求得直线l的方程.
,即可求得直线l的方程.解答:
 解:(1)抛物线y2=8x的焦点为A(2,0),
解:(1)抛物线y2=8x的焦点为A(2,0),∵椭圆
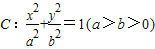 的右顶点A为抛物线y2=8x的焦点
的右顶点A为抛物线y2=8x的焦点∴a=2…(2分)
∵离心率
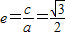 ,∴
,∴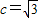 …(3分)
…(3分)故b2=a2-c2=1…(5分)
所以椭圆C的方程为:
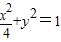 …(6分)
…(6分)(2)设直线
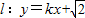
由
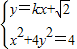 ,消去y可得
,消去y可得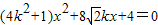 …(8分)
…(8分)因为直线l与椭圆C相交于P,Q两点,所以△=128k2-16(4k2+1)>0
解得
 …(9分)
…(9分)又
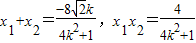 …(10分)
…(10分)设P(x1,y1),Q(x2,y2),PQ中点M(x,y)
因为线段PQ的中点横坐标是
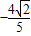 ,所以
,所以 …(12分)
…(12分)解得k=1或
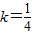 …(13分)
…(13分)因为
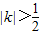 ,所以k=1
,所以k=1因此所求直线
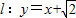 …(14分)
…(14分)点评:本题考查抛物线的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
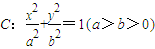 的左顶点A(-2,0),过右焦点F且垂直于长轴的弦长为3.
的左顶点A(-2,0),过右焦点F且垂直于长轴的弦长为3.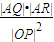 为定值.
为定值. 的右顶点A为抛物线y2=8x的焦点,上顶点为B,离心率为
的右顶点A为抛物线y2=8x的焦点,上顶点为B,离心率为
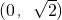 且斜率为k的直线l与椭圆C相交于P,Q两点,若线段PQ的中点横坐标是
且斜率为k的直线l与椭圆C相交于P,Q两点,若线段PQ的中点横坐标是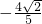 ,求直线l的方程.
,求直线l的方程.