题目内容
 棱长为1的正方体ABCD-A1B1C1D1中,若E,F分别为AA1,C1D1的中点,G是正方形BCC1B1的中心,则空间四边形AEFG在该正方体的面上的正投影的面积最大值为
棱长为1的正方体ABCD-A1B1C1D1中,若E,F分别为AA1,C1D1的中点,G是正方形BCC1B1的中心,则空间四边形AEFG在该正方体的面上的正投影的面积最大值为分析:看出空间四边形AEFG在该正方体的各个面上的投影,看出投影的形状和大小,有两个能够直接做出面积,不能直接作出面积的用正方形面积减去去掉的面积,比较得到结果.
解答:解:空间四边形AEFG在该正方体的下面上的投影是一个等腰三角形,
腰长是
,底边长是面的对角线的一半是
,
∴这个投影的面积是
×
×
=
,
空间四边形AEFG在该正方体的前后面上的投影是一个四边形,
它的面积是1-2×
×
×
-
×1×
=
,
空间四边形AEFG在该正方体的左右面上的投影是一个平行四边形,
它的面积是
×
=
,
综上所述面积最大的是
,
故答案为:
.
腰长是
| ||
| 2 |
| ||
| 2 |
∴这个投影的面积是
| 1 |
| 2 |
3
| ||
| 4 |
| ||
| 2 |
| 3 |
| 8 |
空间四边形AEFG在该正方体的前后面上的投影是一个四边形,
它的面积是1-2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
空间四边形AEFG在该正方体的左右面上的投影是一个平行四边形,
它的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
综上所述面积最大的是
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查平行投影及平行投影作图法,考查一个空间四边形在不同面上的投影不同,得到的面积也不同,本题需要运算.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
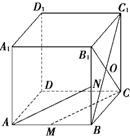 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心. 已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )
已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )