题目内容
7.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量$\overrightarrow m$=(a+b,a-c),$\overrightarrow n$=(sinC,sinA-sinB),且$\overrightarrow m$∥$\overrightarrow n$.(1)求∠B的大小.
(2)若a=1,b=$\sqrt{3}$,求△ABC的面积.
分析 (1)由向量共线和正余弦定理可得cosB,进而可得角B;
(2)由余弦定理解方程可得c值,代入三角形的面积公式S=$\frac{1}{2}$acsinB计算可得.
解答 解:(1)由题意结合向量共线可得(a+b)(sinA-sinB)=(a-c)sinC,
由正弦定理可得(a+b)(a-b)=(a-c)c,
整理可得a2-b2=ac-c2,即a2+c2-b2=ac,
∴由余弦定理可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,
∵B为三角形的内角,∴B=60°;
(2)由余弦定理可得b2=a2+c2-2accosB,
代值可得3=1+c2-c,解方程可得c=2,
∴△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}×1×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查解三角形,涉及正余弦定理和三角形的面积公式以及向量的平行关系,属中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
18.已知定义在R上的函数f(x)满足如下条件:①函数f(x)的图象关于y轴对称;②对于任意x∈R,f(2+x)-f(2-x)=0;③当x∈[0,2]时,f(x)=x.若过点(-1,0)的直线l与函数y=f(x)的图象在x∈[0,16]上恰有8个交点,在直线l斜率k的取值范围是( )
| A. | ($\frac{2}{19}$,$\frac{2}{15}$) | B. | (0,$\frac{15}{2}$) | C. | (0,$\frac{2}{17}$) | D. | (0,$\frac{17}{2}$) |
2.已知数列{an}的前n项和为Sn,当Sn=n2-n时,a5=( )
| A. | 20 | B. | 12 | C. | 8 | D. | 4 |
17.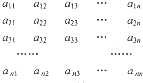 如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
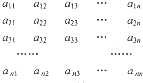 如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )| A. | $\frac{1031}{512}$ | B. | $\frac{1031}{512}$ | C. | $\frac{1013}{1024}$ | D. | $\frac{1031}{1024}$ |
 如图所示,已知椭圆C:$\frac{x^2}{4}$+y2=1左、右端点分别为A1,A2,过定点(1,0)的动直线与椭圆C交于P,Q两点.直线A1P与A2Q交于点S.
如图所示,已知椭圆C:$\frac{x^2}{4}$+y2=1左、右端点分别为A1,A2,过定点(1,0)的动直线与椭圆C交于P,Q两点.直线A1P与A2Q交于点S.