题目内容
设 与
与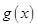 是定义在同一区间
是定义在同一区间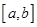 上的两个函数,若函数
上的两个函数,若函数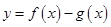 在
在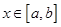 上有两个不同的零点,则称
上有两个不同的零点,则称 和
和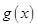 在
在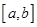 上是“关联函数”,区间
上是“关联函数”,区间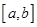 称为“关联区间”.若
称为“关联区间”.若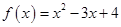 与
与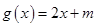 在
在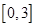 上是“关联函数”,则
上是“关联函数”,则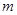 的取值范围为 ( )
的取值范围为 ( )
A.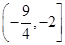 | B.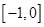 | C.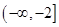 | D.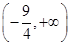 |
A
解析试题分析:令 ,得
,得 ,即
,即 ,即
,即 ,若函数
,若函数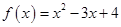 与
与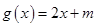 在
在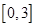 上是“关联函数”,则问题转化为直线
上是“关联函数”,则问题转化为直线 与曲线
与曲线 在区间
在区间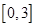 上有两个交点,在同一坐标系中作出直线
上有两个交点,在同一坐标系中作出直线 与曲线
与曲线 在区间
在区间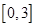 图象,由图象知,当
图象,由图象知,当 时,直线
时,直线 与曲线
与曲线 在区间
在区间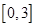 上有两个交点,故选A.
上有两个交点,故选A.
考点:1.新定义;2.函数的零点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数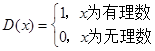 ,则下列结论错误的是( )
,则下列结论错误的是( )
| A.D(x)的值域为{0,1} | B.D(x)是偶函数 |
| C.D(x)不是周期函数 | D.D(x)不是单调函数 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
A.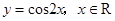 | B.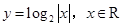 且 且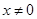 |
C.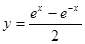 , ,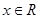 | D.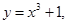 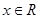 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为 ( )
A.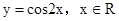 | B.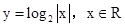 且x≠0 且x≠0 |
C.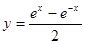 , x , x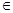 R R | D.y=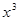 +1, x +1, x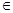 R R |
已知函数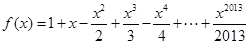 且函数
且函数 的零点均在区间
的零点均在区间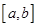
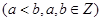 内,圆
内,圆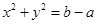 的面积的最小值是( )
的面积的最小值是( )
A.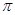 | B.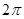 | C. | D.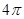 |
已知函数 则
则 ,
, ,
, 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D. |
若 为奇函数且在
为奇函数且在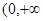 )上递增,又
)上递增,又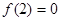 ,则
,则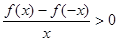 的解集是( )
的解集是( )
A. | B.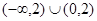 |
C.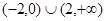 | D.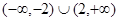 |
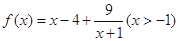 ,当x=a时,
,当x=a时,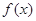 取得最小值,则在直角坐标系中,函数
取得最小值,则在直角坐标系中,函数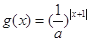 的大致图象为( )
的大致图象为( )

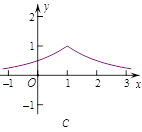
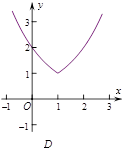
 的图象可能是 ( )
的图象可能是 ( ) 