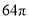题目内容
已知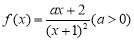 .
.
(Ⅰ)若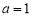 ,求
,求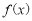 在
在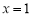 处的切线方程;
处的切线方程;
(Ⅱ)确定函数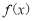 的单调区间,并指出函数
的单调区间,并指出函数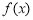 是否存在最大值或最小值.
是否存在最大值或最小值.
(Ⅰ)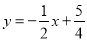 ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
试题分析:(Ⅰ)当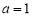 时,
时,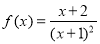 ,容易算得
,容易算得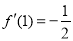 ,由
,由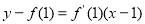 得切线方程为
得切线方程为 ;(Ⅱ)
;(Ⅱ)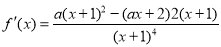 =
=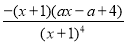 ,令
,令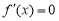 ,得
,得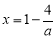 ,注意到
,注意到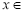
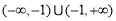 ,所以需分类讨论:当
,所以需分类讨论:当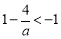 ,即
,即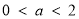 时,
时,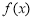 的增区间是
的增区间是 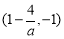 ,减区间是
,减区间是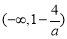 和
和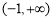 ,当
,当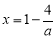 时,取得极小值
时,取得极小值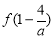 ;当
;当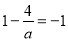 即
即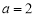 时,
时,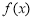 的减区间是
的减区间是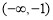 和
和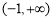 ,
,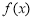 无最大值和最小值;当
无最大值和最小值;当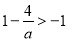 即
即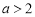 时,
时,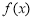 的增区间是
的增区间是 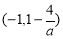 ,减区间是
,减区间是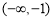 和
和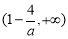 ,当
,当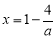 时,取得极大值
时,取得极大值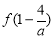
试题解析:(Ⅰ)当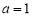 时,
时,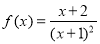 ,
,
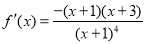 2分
2分
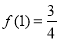 ,
,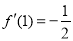 3分
3分
所以直线方程为 ,
,
即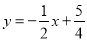 4分
4分
(Ⅱ)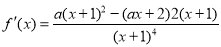 =
=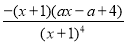
其中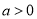 ,
,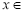
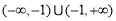 2分
2分
令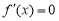 ,得
,得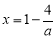
当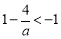 ,即
,即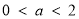 时,
时,
|
|
|
|
|
| 小于0 | 等于0 | 大于0 | 小于0 |
| 递减 | 极小值 | 递增 | 递减 |
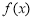 的增区间是
的增区间是 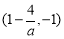 ,减区间是
,减区间是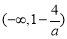 和
和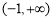 ,当
,当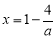 时,取得极小值
时,取得极小值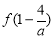 。又
。又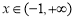 时,
时,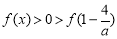 ,所以
,所以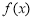 有最小值
有最小值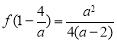 ; 6分
; 6分
当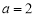 时,
时,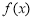 的减区间是
的减区间是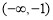 和
和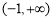 ,
,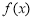 无最大值和最小值。 7分
无最大值和最小值。 7分
3)当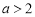 时,
时,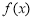 的增区间是
的增区间是 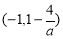 ,减区间是
,减区间是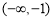 和
和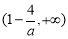 ,当
,当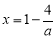 时,取得极大值
时,取得极大值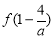 。又
。又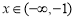 时,
时,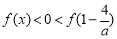 ,所以
,所以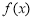 有最大值
有最大值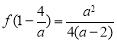 。 9分
。 9分
考点:导数及其综合应用

练习册系列答案
相关题目



 ,则此函数的值域为( )
,则此函数的值域为( ) B.
B. C.
C. D.
D.
 是奇函数,当
是奇函数,当 时,
时, ,则
,则 = .
= . ,则四面体
,则四面体 的体积为 .
的体积为 . 是
是 的 条件.(在充分不必要,必要不充分,充要,既不充分又不必要中选一个填写)
的 条件.(在充分不必要,必要不充分,充要,既不充分又不必要中选一个填写) 中,
中, ,
, ,
, ,
, ,设
,设
 ,则
,则 的取值范围是 .
的取值范围是 .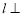 平面
平面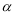 ,直线
,直线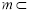 平面
平面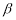 ,有下列四个命题:①若
,有下列四个命题:①若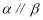 ,则
,则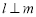 ;
;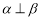 ,则
,则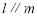 ;③若
;③若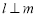 ,则
,则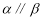 .
.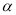 的顶点在坐标原点,始边与
的顶点在坐标原点,始边与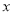 轴的非负半轴重合,终边经过点
轴的非负半轴重合,终边经过点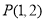 ,则
,则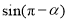 的值是 .
的值是 .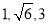 ,则这个球的表面积为( )
,则这个球的表面积为( )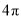 B.
B.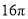 C.
C.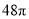 D.
D.