Question

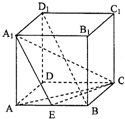如图，在正方体ABCD-A₁B₁C₁D₁中，E为AB的中点．
（1）求异面直线BD₁与CE所成角的余弦值；
（2）求二面角A₁-EC-A的余弦值．

Answer 1

分析：由题设条件知，本题有同一点出发的三条两两垂直的线段，故可以建立空间坐标系，利用向量法求得两异面直线的夹角及二面角的夹角余弦值．由图，可以D为原点，DC为y轴，DA为x轴，DD₁为Z轴建立空间直角坐标系，给出各点的坐标
（1）由图给出异面直线BD₁与CE的方向向量，由数量积公式求出两直线的夹角；
（2）由向量运算求出两个平面的法向量，再由数量积公式求出两个平面的夹角的余弦值

解答：解：以D为原点，DC为y轴，DA为x轴，DD₁为Z轴建立空间直角坐标系，…（1分）
则A₁（1，0，1），B（1，1，0），C（0，1，0），D₁（0，0，1），E(1，

1

2

，0)，…（2分）
（1）

BD1

=(-1，-1，1)，

CE

=(1，-

1

2

，0)…（1分）
cos＜

BD1

，

CE

＞=-

15

15

，…（1分）
所以所求角的余弦值为

15

15

…（1分）
（2）D₁D⊥平面AEC，所以

D1D

为平面AEC的法向量，

D1D

=(0，0，1)…（1分）
设平面A₁EC法向量为

n

=(x，y，z)，又

A1E

=(0，

1

2

，-1)，

A1C

=(-1，1，-1)，

n • A1E =0 n • A1C =0

即

1 2 y-z=0 -x+y-z=0

，取

n

=(1，2，1)，…（3分）
所以cos＜

DD1

，

n

＞=

6

6

…（2分）

点评：本题考查用空间向量求二面角的夹角与两直线的夹角，解题的关键是建立恰当的坐标系，及掌握向量法求线线角，面面角的向量公式，本题考查了数形结合的思想及转化的思想，利用向量求解决立体几何问题是近几年高考的热点，向量法解决立体几何问题降低了思维难度，化推理为计算，使得几何求解变得简单，此法也有不足，需要建立坐标系，且运算量较大