题目内容
设函数f(x)= ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
| A.x1+x2>0,y1+y2>0 |
| B.x1+x2<0,y1+y2>0 |
| C.x1+x2>0,y1+y2<0 |
| D.x1+x2<0,y1+y2<0 |
C
解析

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下列说法正确的是( )
A.幂函数的图像恒过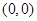 点 点 | B.指数函数的图像恒过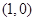 点 点 |
C.对数函数的图像恒在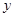 轴右侧 轴右侧 | D.幂函数的图像恒在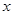 轴上方 轴上方 |
已知函数 ,若a,b,c互不相等,且
,若a,b,c互不相等,且 ,则
,则 的取值范围为( )
的取值范围为( )
A. | B. |
C. | D. |
已知A={x| ,x∈R},B={x||x-i|<
,x∈R},B={x||x-i|< ,i为虚数单位,x>0},则A
,i为虚数单位,x>0},则A B=( )
B=( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
已知函数 ,在区间
,在区间 内存在
内存在 使
使 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
设a= 0.5,b=
0.5,b= 0.4,c=log
0.4,c=log (log34),则( )
(log34),则( )
| A.c<b<a | B.a<b<c |
| C.c<a<b | D.a<c<b |
设a=log32,b=log52,c=log23,则( ).
| A.a>c>b | B.b>c>a | C.c>b>a | D.c>a>b |
若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间 ( ).
| A.(a,b)和(b,c)内 | B.(-∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 | D.(-∞,a)和(c,+∞)内 |
已知符号函数sgn(x)= 则函数f(x)=sgn(ln x)-ln2x的零点个数为 ( ).
则函数f(x)=sgn(ln x)-ln2x的零点个数为 ( ).
| A.1 | B.2 | C.3 | D.4 |