题目内容
已知点 满足椭圆方程
满足椭圆方程 ,则
,则 的最大值为
的最大值为
【答案】

【解析】
试题分析:∵p(x,y)在椭圆 上
上
∴ 即椭圆上点(x,y)到点(1,0)的斜率
即椭圆上点(x,y)到点(1,0)的斜率
即过点(1,0)且与椭圆有交点的直线L:y=k(x-1)的斜率
又直线的变化范围为从与椭圆在第一象限相切到与椭圆在第四象限相切(可画图更易理解)欲求得变化范围只需求出当过点(1,0)的直线与椭圆相切时的斜率k
即直线L与椭圆只有一个交点
联立 ,y=k(x-1)
,y=k(x-1)
得2x²+(k(x-1))²=1
即(2+k²)x²-2k²x+k²-1=0
 ,
,
即
即-k²+2=0
解k=±
∴当直线与椭圆相切时k=± ,即
,即 的最大值为
的最大值为 。
。
考点:本题主要考查直线与椭圆的位置关系,斜率的概念及计算。
点评:典型题,关键是理解 的意义并运用数形结合思想解题。
的意义并运用数形结合思想解题。

练习册系列答案
相关题目
 是椭圆
是椭圆 的右焦点,点
的右焦点,点 、
、 分别是
分别是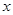 轴、
轴、 轴上的动点,且满足
轴上的动点,且满足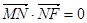 .若点
.若点 满足
满足 .
. 的方程;
的方程; 、
、 两点,直线
两点,直线 、
、 与直线
与直线 分别交于点
分别交于点 、
、 (
( 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由. 是椭圆
是椭圆 的右焦点,点
的右焦点,点 、
、 分别是
分别是 轴、
轴、 轴上的动点,且满足
轴上的动点,且满足 .若点
.若点 满足
满足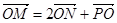 .
. 的方程;
的方程; 、
、 两点,直线
两点,直线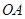 、
、 与直线
与直线 分别交于点
分别交于点 、
、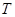 (
( 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由. 分别是椭圆
分别是椭圆
 的左、右
焦点,已知点
的左、右
焦点,已知点 满足
满足 ,且
,且 。设
。设 是上半椭圆上且满足
是上半椭圆上且满足 的两点。
的两点。 ,求直线AB的斜率。
,求直线AB的斜率。 分别是椭圆
分别是椭圆
 的左、右
焦点,已知点
的左、右
焦点,已知点 满足
满足 ,且
,且 。设
。设 是上半椭圆上且满足
是上半椭圆上且满足 的两点。
的两点。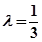 ,求直线AB的斜率。
,求直线AB的斜率。