题目内容
设α、β∈(0,π),且sin(α+β)=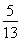 ,tan
,tan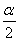 =
=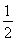 ,则cosβ=________.
,则cosβ=________.
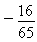
【解析】∵tan =
=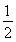 ,∴tanα=
,∴tanα= =
= ,而α∈(0,π),∴α∈
,而α∈(0,π),∴α∈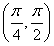 .由tanα=
.由tanα= =
=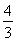 及sin2α+cos2α=1得sinα=
及sin2α+cos2α=1得sinα=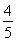 ,cosα=
,cosα=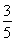 ;又sin(α+β)=
;又sin(α+β)=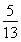 <
< ,∴α+β∈(
,∴α+β∈(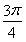 ,π),cos(α+β)=-
,π),cos(α+β)=-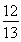 .
.
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
设α、β∈(0,π),且sin(α+β)=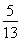 ,tan
,tan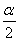 =
=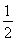 ,则cosβ=________.
,则cosβ=________.
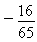
【解析】∵tan =
=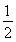 ,∴tanα=
,∴tanα= =
= ,而α∈(0,π),∴α∈
,而α∈(0,π),∴α∈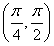 .由tanα=
.由tanα= =
=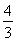 及sin2α+cos2α=1得sinα=
及sin2α+cos2α=1得sinα=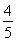 ,cosα=
,cosα=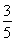 ;又sin(α+β)=
;又sin(α+β)=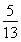 <
< ,∴α+β∈(
,∴α+β∈(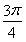 ,π),cos(α+β)=-
,π),cos(α+β)=-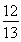 .
.
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-

 名校课堂系列答案
名校课堂系列答案