题目内容
假定某射手每次射击命中的概率为 ,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,
,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:(1)目标被击中的概率;
(2)X的概率分布;
(3)均值E(X).
【答案】分析:(1)由题意可得:目标没有被击中的概率为: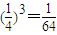 ,再根据对立事件的根据公式可得答案.
,再根据对立事件的根据公式可得答案.
(2)X可能取的值为:1,2,3.再根据题意分别求出其发生的概率,进而求出X的分布列.
(3)结合(2)并且根据数学期望的有关公式可得答案.
解答:解:(1)由题意可得:目标没有被击中的概率为: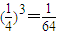 ,
,
所以目标被击中的概率为:1-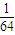 =
= .
.
(2)X可能取的值为:1,2,3.
所以P(X=1)= ,P(X=2)=
,P(X=2)= ,P(X=3)=
,P(X=3)= =
= ,
,
所以X的分布列为:
(3)由(2)可得:均值E(X)= =
= .
.
点评:本题在解题过程中当随机变量为3时,题目容易出错,我们模拟一下当时的情况,三颗子弹都用上说明前两次都没有射中,而第三次无论是否射中,子弹都为0.
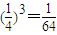 ,再根据对立事件的根据公式可得答案.
,再根据对立事件的根据公式可得答案.(2)X可能取的值为:1,2,3.再根据题意分别求出其发生的概率,进而求出X的分布列.
(3)结合(2)并且根据数学期望的有关公式可得答案.
解答:解:(1)由题意可得:目标没有被击中的概率为:
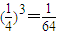 ,
,所以目标被击中的概率为:1-
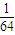 =
= .
.(2)X可能取的值为:1,2,3.
所以P(X=1)=
 ,P(X=2)=
,P(X=2)= ,P(X=3)=
,P(X=3)= =
= ,
,所以X的分布列为:
| X | 1 | 2 | 3 |
| P |  |  | 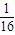 |
 =
= .
.点评:本题在解题过程中当随机变量为3时,题目容易出错,我们模拟一下当时的情况,三颗子弹都用上说明前两次都没有射中,而第三次无论是否射中,子弹都为0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,且只有
,且只有 发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
 .
. ,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,
,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,