题目内容
【题目】设数列{an}的前n项和为Sn , 且满足Sn=2﹣an , n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an , 求数列{bn}的通项公式;
(3)设cn= ![]() ,数列{cn}的前n项和为Tn=
,数列{cn}的前n项和为Tn= ![]() .求n.
.求n.
【答案】
(1)解:当n=1时,S1=a1=2﹣a1,所以a1=1.
当n≥2时,Sn﹣1=2﹣an﹣1,且Sn=2﹣an,
所以an=2(2﹣an)﹣(2﹣an﹣1)得:an= ![]() an﹣1,
an﹣1,
则数列{an}是以1为首项, ![]() 为公比的等比数列,
为公比的等比数列,
∴数列{an}的通项公式是an=( ![]() )n﹣1
)n﹣1
(2)解:由bn+1=bn+an,且an=( ![]() )n﹣1,
)n﹣1,
∴bn+1﹣bn=( ![]() )n﹣1,
)n﹣1,
则b2﹣b1=( ![]() )0,b3﹣b2=(
)0,b3﹣b2=( ![]() )1,b4﹣b3=(
)1,b4﹣b3=( ![]() )2,…,bn﹣bn﹣1=(
)2,…,bn﹣bn﹣1=( ![]() )n﹣2,
)n﹣2,
以上n个等式叠加得:bn﹣b1=( ![]() )0+(
)0+( ![]() )1+(
)1+( ![]() )2+…+(
)2+…+( ![]() )n﹣2=
)n﹣2= 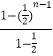 =2[1﹣(
=2[1﹣( ![]() )n﹣1]
)n﹣1]
=2﹣ ![]() ,
,
∵b1=1,
∴bn=3﹣ ![]()
(3)解:由题意知 ![]() .
.
则Tn=4﹣ ![]() =
= ![]() ,
,
∵Tn+1﹣Tn=(4﹣ ![]() )﹣(4﹣
)﹣(4﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() =
= ![]() >0,
>0,
∴Tn<Tn+1恒成立,
∵T6=4﹣ ![]() =
= ![]() ,
,
∴n=6.
【解析】(1)由已知条件推导出{an}是以1为首项, ![]() 为公比的等比数列,由此能求出数列{an}的通项公式.(2)由bn+1=bn+an , 且an=(
为公比的等比数列,由此能求出数列{an}的通项公式.(2)由bn+1=bn+an , 且an=( ![]() )n﹣1 . 知bn+1﹣bn=(
)n﹣1 . 知bn+1﹣bn=( ![]() )n﹣1 , 由此利用叠加法能求出bn=3﹣
)n﹣1 , 由此利用叠加法能求出bn=3﹣ ![]() .(3)根据已知条件推知Tn+1﹣Tn=(4﹣
.(3)根据已知条件推知Tn+1﹣Tn=(4﹣ ![]() )﹣(4﹣
)﹣(4﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() =
= ![]() >0,所以求得shiftTn<Tn+1恒成立的n的值即可.
>0,所以求得shiftTn<Tn+1恒成立的n的值即可.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系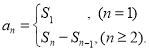 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为
精确到0.1),若某天的气温为![]() ,预测这天热奶茶的销售杯数;
,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取两天,求所选取两天中至少有一天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .
.
参考公式: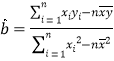 ,
,![]() .
.

