题目内容
在极坐标系xoy中,定点A(2,π),动点B在直线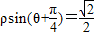 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 .
【答案】分析:先利用三角函数的和角公式展开曲线C的极坐标方程的左式,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.将直线的极坐标方程化成直角坐标方程,再在直角坐标系中算出点到直线的距离,即线段AB的最短长度.
解答:解:直线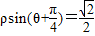 的直角坐标方程为:
的直角坐标方程为:
x+y-1=0,
定点A(2,π)的直角坐标(-2,0),
它到直线的距离:
d=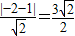 .
.
则线段AB的最短长度为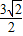 .
.
故答案为: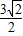 .
.
点评:本小题主要考查简单曲线的极坐标方程,属于基础题.能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
解答:解:直线
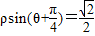 的直角坐标方程为:
的直角坐标方程为:x+y-1=0,
定点A(2,π)的直角坐标(-2,0),
它到直线的距离:
d=
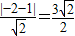 .
.则线段AB的最短长度为
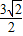 .
.故答案为:
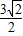 .
.点评:本小题主要考查简单曲线的极坐标方程,属于基础题.能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 . 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 . 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 . 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 .