题目内容
集合M={y|y=
，x，y∈N}的元素个数是（ ）
| 8 | x+3 |
分析：根据题中给出的条件，x，y∈N，分别从最小的自然数0开始给x代值，求相应的y的值，直到得出的y＜1为止，求出y∈N的个数．
解答：解：因为M={y|y=
，x，y∈N}，
所以，当x=0时，y=
∉N；
当x=1时，y=
=2∈N；
当x=2时，y=
=
∉N；
当x=3时，y=
=
∉N；
当x=4时，y=
=
∉N；
当x=5时，y=
=1∈N；
当x≥6时，y=
＜1，所以y∉N．
综上，M={y|y=
，x，y∈N}={2，1}，元素个数是2个．
故选A．
| 8 |
| x+3 |
所以，当x=0时，y=
| 8 |
| 3 |
当x=1时，y=
| 8 |
| 1+3 |
当x=2时，y=
| 8 |
| 2+3 |
| 8 |
| 5 |
当x=3时，y=
| 8 |
| 3+3 |
| 4 |
| 3 |
当x=4时，y=
| 8 |
| 4+3 |
| 8 |
| 7 |
当x=5时，y=
| 8 |
| 5+3 |
当x≥6时，y=
| 8 |
| x+3 |
综上，M={y|y=
| 8 |
| x+3 |
故选A．
点评：本题考查了集合中元素的个数，考查了用赋值法分析和解决问题，属基础题型．
练习册系列答案
巧学巧练系列答案
相关题目
N的真子集个数是( )
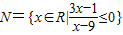，则M∩N的真子集的个数是（ ）