题目内容
椭圆E的中心在原点O,焦点在x轴上,其离心率e=(1)用直线l的斜率k(k≠0)表示△OAB的面积;
(2)当△OAB的面积最大时,求椭圆E的方程.
解:(1)设椭圆E的方程为![]() +
+![]() =1,(a>b>0),由e=
=1,(a>b>0),由e=![]() =
=![]() 得,a2=3b2.
得,a2=3b2.
故椭圆方程为x2+3y2=3b2.
设A(x1,y1)、B(x2、y2).由于点C(-1,0)分向量![]() 的比为2,
的比为2,
∴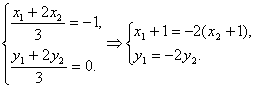
由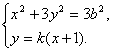
![]() (3k2+1)x2+6k2x+3k2-3b2=0.
(3k2+1)x2+6k2x+3k2-3b2=0.
由直线l与椭圆E相交于A(x1,y1)、B(x2,y2)两点得:

而S△OAB=![]() |y1-y2|=
|y1-y2|=![]() |-2y2-y2|=
|-2y2-y2|=![]() |y2|=
|y2|=![]() |k(x2+1)|, ①
|k(x2+1)|, ①
由![]() =-1和x1+x2=
=-1和x1+x2=![]() 得x2+1=
得x2+1=![]() ,把其代入①得:
,把其代入①得:
S△OAB=![]() (k≠0).
(k≠0).
(2)因S△OAB=![]() =
=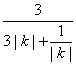 ≤
≤![]() =
=![]() ,当且仅当k=±
,当且仅当k=±![]() 时,S△OAB取得最大值,此时x1+x2=-1.
时,S△OAB取得最大值,此时x1+x2=-1.
又∵![]() =1,∴x2=-3,x1=1,将x1=1,x2=-3,k=±
=1,∴x2=-3,x1=1,将x1=1,x2=-3,k=±![]() 代入x1x2=
代入x1x2=![]() ,
,
得3b2=5.
∴椭圆方程为x2+3y2=5.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 ,过点C(-1,0)的直线
,过点C(-1,0)的直线 交椭圆于A,B两点,且满足
交椭圆于A,B两点,且满足 ,
, 为常数。
为常数。 时,求三角形OAB的面积.
时,求三角形OAB的面积.  ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足: (λ≥2).
(λ≥2).