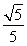题目内容
已知抛物线C∶y2=4x的焦点为F，过点F的直线l与C相交于两点A、B.（1）若|AB|=
，求直线l的方程；
（2）求|AB|的最小值.
解：（1）设l的方程为x+my-1=0，代入y2=4x.?
∴y2+4my-4=0.?
设A（x1,y1），B（x2,y2），则y1+y2=-4m.?
根据抛物线定义，?
|AB|=x1+x2+p=x1+x2+2=（1-my1）+（1-my2）+2=4（m2+1）.?
若|AB|=163，则4（m2+1）=,m=±
，?
即直线l的方程为x±
y-1=0.?
（2）由（1）知|AB|=4（m2+1）≥4,当且仅当m=0时，|AB|有最小值4.
练习册系列答案
相关题目
|AF|，则△AFK的面积为
