题目内容
(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系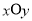 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
,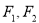 是圆锥曲线
是圆锥曲线 的左、右焦点.
的左、右焦点.
(1)以坐标原点为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程;
(2)设(1)中直线 与圆锥曲线
与圆锥曲线 交于
交于 两点,求
两点,求 .
.
(1)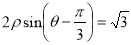 ;(2)
;(2) .
.
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若 有范围限制,要标出
有范围限制,要标出 的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式
的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式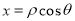 及
及 直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如
直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如 ,
, ,
, 的形式,进行整体代换,其中方程的两边同乘以(或同除以)
的形式,进行整体代换,其中方程的两边同乘以(或同除以) 及方程的两边平方是常用的变形方法.
及方程的两边平方是常用的变形方法.
试题解析:【解析】
(1)圆锥曲线 的参数方程为
的参数方程为
 (
( 为参数),
为参数),
所以普通方程为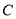 :
: 2分
2分
 3分
3分
 直线极坐标方程为:
直线极坐标方程为: 5分
5分
(2)直线的参数方程是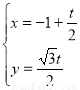 (为参数), 7分
(为参数), 7分
代入椭圆方程得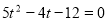 8分
8分
 9分
9分
 10分
10分
考点:1、极坐标方程的应用;2、直线与椭圆的位置关系.

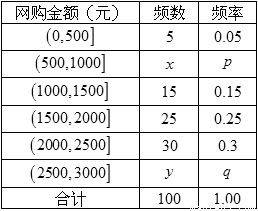
(本小题满分12分)2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达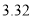 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为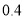 .
.


(1)确定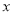 ,
, ,
,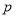 ,
, 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
①请将列联表补充完整;
网龄3年以上 | 网龄不足3年 | 合计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
合计 | 100 |
②并据此列联表判断,是否有 %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: ,其中
,其中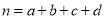 )
)
(本小题满分12分)2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达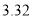 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为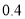 .
.

确定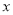 ,
,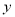 ,
,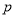 ,
,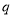 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
(1)请将列联表补充完整;
网龄3年以上 | 网龄不足3年 | 合计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
合计 | 100 |
(2)并据此列联表判断,是否有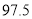 %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: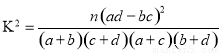 ,其中
,其中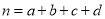 )
)
 的直线
的直线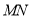 与双曲线
与双曲线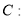
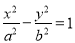 交于
交于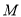 、
、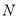 两点,
两点,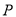 是双曲线
是双曲线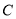 上异于
上异于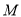 、
、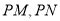 的斜率之积
的斜率之积 ,则双曲线
,则双曲线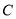 的离心率
的离心率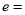
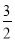 B.
B. C.
C.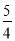 D.2
D.2

 B.
B. C.
C. D.
D.
 = .
= . = (m2,4),
= (m2,4), =(1,1)则“m= -2”是“
=(1,1)则“m= -2”是“















 是
是 的重心,
的重心, ,
, ,
, 分别是角
分别是角 的对边,若
的对边,若 ,则角
,则角 ( )
( ) B.
B. C.
C. D.
D.
















 ,
, ,设
,设 ,
, ,
, ,则
,则 的最小值为 .
的最小值为 .