题目内容

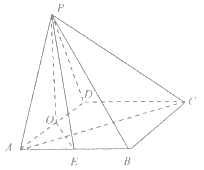
【题目】在四棱锥中，底面，底面为正方形，，点为正方形内部的一点，且，则直线与所成角的余弦值的取值范围为( )

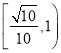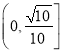A.B.C.D.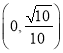

【答案】D

【解析】

根据题意，建立空间直角坐标系，在平面上，由计算的轨迹方程，可知的轨迹是以为圆心，以2为半径的圆，在正方形中的部分；根据平行找直线与所成角的平面角，根据的轨迹判定临界值，从而确定直线与所成角的余弦值的取值范围.

由题意，以为坐标原点，分别以为轴，建立空间直角坐标系，如图所示，则有，

设，由，则列方程有

化简得，即点的轨迹是以为圆心，以2为半径的圆，在正方形中的部分；

过作垂足为,连接，则有

则直线与所成角的平面角为，

则

根据点的轨迹是以为圆心，以2为半径的圆，在正方形中的部分，

则点轨迹与正方形的边交于一点，记为

与正方形的边交于一点，记为

当点从运动到位置时，逐渐减小，逐渐增大，则的取值逐渐减小，

计算，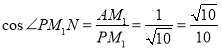

则直线与所成角的余弦值的取值范围是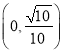

故选：

练习册系列答案
相关题目

【题目】甲乙两人报名参加由某网络科技公司举办的“技能闯关”双人电子竞技比赛，比赛规则如下：每一轮“闯关”结果都采取计分制，若在一轮闯关中，一人过关另一人未过关，过关者得1分，未过关得分；若两人都过关或都未过关则两人均得0分.甲、乙过关的概率分别为和，在一轮闯关中，甲的得分记为.

（1）求的分布列；

（2）为了增加趣味性，系统给每位报名者基础分3分，并且规定出现一方比另一方多过关三轮者获胜，此二人比赛结束.表示“甲的累积得分为时，最终认为甲获胜”的概率，则，其中，，，令.证明：点的中点横坐标为；

（3）在第（2）问的条件下求，并尝试解释游戏规则的公平性.

【题目】已知数列是递减的等差数列，的前项和是，且，有以下四个结论：

①；

②若对任意都有成立，则的值等于7或8时；

③存在正整数，使；

④存在正整数，使．

其中所有正确结论的序号是

A. ①②B. ①②③

C. ②③④D. ①②③④

【题目】已知函数（）.

（1）当时，求函数的最小值；

（2）若时，，求实数的取值范围.

【题目】在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，P是曲线上的动点，M为线段OP的中点，设点M的轨迹为曲线．

（1）求的极坐标方程；

（2）若射线与曲线异于极点的交点为A，与曲线异于极点的交点为B，求．

【题目】已知函数ae2x+(a﹣2) ex﹣x.

（1）讨论的单调性；

（2）若有两个零点，求a的取值范围.

【题目】已知函数，为的导数．

（Ⅰ）求曲线在点处的切线方程；

（Ⅱ）证明：在区间上存在唯一零点；

（Ⅲ）设，若对任意，均存在，使得，求实数的取值范围.

【题目】已知函数，其中，为自然对数的底数.

（1）当时，证明：对；

（2）若函数在上存在极值，求实数的取值范围。

【题目】如图，四棱锥的底面是菱形，底面，分别是的中点，，，.

（I）证明：；

（II）求直线与平面所成角的正弦值；

（III）在边上是否存在点，使与所成角的余弦值为，若存在，确定点位置；若不存在，说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网