题目内容
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是
- A.(1-
 ,2)
,2) - B.(0,2)
- C.(
 -1,2)
-1,2) - D.(0,1+
 )
)
A
分析:由A,B及△ABC为正三角形可得,可求C的坐标,然后把三角形的各顶点代入可求z的值,进而判断最大与最小值,即可求解范围
解答: 解:设C(a,b),(a>0,b>0)
解:设C(a,b),(a>0,b>0)
由A(1,1),B(1,3),及△ABC为正三角形可得,AB=AC=BC=2
即(a-1)2+(b-1)2=(a-1)2+(b-3)2=4
∴b=2,a=1+ 即C(1+
即C(1+ ,2)
,2)
则此时直线AB的方程x=1,AC的方程为y-1= (x-1),直线BC的方程为y-3=(
(x-1),直线BC的方程为y-3=(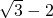 )(x-1)
)(x-1)
当直线x-y+z=0经过点A(1,1)时,z=0,经过点B(1,3)z=2,经过点C(1+ ,2)时,z=1-
,2)时,z=1-
∴
故选A
点评:考查学生线性规划的理解和认识,考查学生的数形结合思想.属于基本题型.
分析:由A,B及△ABC为正三角形可得,可求C的坐标,然后把三角形的各顶点代入可求z的值,进而判断最大与最小值,即可求解范围
解答:
 解:设C(a,b),(a>0,b>0)
解:设C(a,b),(a>0,b>0)由A(1,1),B(1,3),及△ABC为正三角形可得,AB=AC=BC=2
即(a-1)2+(b-1)2=(a-1)2+(b-3)2=4
∴b=2,a=1+
 即C(1+
即C(1+ ,2)
,2)则此时直线AB的方程x=1,AC的方程为y-1=
 (x-1),直线BC的方程为y-3=(
(x-1),直线BC的方程为y-3=(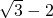 )(x-1)
)(x-1)当直线x-y+z=0经过点A(1,1)时,z=0,经过点B(1,3)z=2,经过点C(1+
 ,2)时,z=1-
,2)时,z=1-
∴

故选A
点评:考查学生线性规划的理解和认识,考查学生的数形结合思想.属于基本题型.

练习册系列答案
相关题目
已知正三角形ABC的边长为a,那么三角形ABC根据斜二测画法得到的平面直观图三角形A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知正三角形ABC的边长为1,且
=
,
=
,则|
-
|=( )
| BA |
| a |
| AC |
| b |
| a |
| b |
A、
| ||
| B、3 | ||
C、
| ||
| D、1 |
 如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则
如图,已知正三角形ABC的边长为2,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则