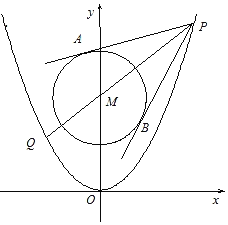
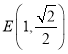题目内容
【题目】已知椭圆
的离心率为
，直线
，圆
的方程为
，直线
被圆截得的弦长与椭圆
的短轴长相等，椭圆的左顶点为
，上顶点为
.
（1）求椭圆的方程；
（2）已知经过点
且斜率为
直线与椭圆有两个不同的交点
和
，请问是否存在常数
，使得向量
与
共线？如果存在，求出的值；如果不存在，请说明理由.
【答案】（1）
（2）不存在；详见解析
【解析】
（1）求得圆心到直线的距离，利用直线和圆相交所得弦长公式列方程，解方程求得
的值，结合椭圆离心率以及
，求得
的值，进而求得椭圆离心率.
（2）设出直线
的方程，联立直线的方程和椭圆的方程，写出根于系数关系以及判别式，利用
与
共线以及向量共线的坐标表示列方程，由此判断出不存在符合题意的常数
.
（1）圆心
到直线的距离为
，
直线被圆截得的弦长
，
.
由椭圆离心率为
，结合可得
，
.即椭圆
的方程为：.
（2）设直线的方程为
，
代入椭圆方程，整理，得
，①
因为直线与椭圆有两个不同的交点
和
等价于
，
解得
.
设
，
，则
，
由①得
，②
又
，③
因为
，所以
.
所以与共线等价于
.
将②③代入上式，解得
，
（舍）.
因为不满足，
所以不存在常数，使得向量与共线.
【题目】某工厂的
,
,
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自,,各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
【题目】已知椭圆C的中心在坐标原点，焦点在x轴上，它的一个顶点恰好是抛物线
的焦点，离心率为
.
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过椭圆C的右焦点F作直线l交椭圆C于A、B两点，交y轴于M点，若
，
，求
的值.
【题目】随着食品安全问题逐渐引起人们的重视，有机、健康的高端绿色蔬菜越来越受到消费者的欢迎，同时生产—运输—销售一体化的直销供应模式,不仅减少了成本，而且减去了蔬菜的二次污染等问题.
（1）在有机蔬菜的种植过程中，有机肥料使用是必不可少的.根据统计某种有机蔬菜的产量与有机肥料的用量有关系，每个有机蔬菜大棚产量的增加量
（百斤）与使用堆沤肥料
（千克）之间对应数据如下表
使用堆沤肥料 | 2 | 4 | 5 | 6 | 8 |
产量的增加量 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据，用最小二乘法求出关于的线性回归方程
；并根据所求线性回归方程，估计如果每个有机蔬菜大棚使用堆沤肥料10千克，则每个有机蔬菜大棚产量增加量是多少百斤?
（2）某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装,以每份10元的价格销售到生鲜超市.“乐购”生鲜超市以每份15元的价格卖给顾客，如果当天前8小时卖不完，则超市通过促销以每份5元的价格卖给顾客（根据经验，当天能够把剩余的有机蔬菜都低价处理完毕，且处理完毕后，当天不再进货）.该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量（单位:份），制成如下表格(注:
，且
)；
前8小时内的销售量（单位:份） | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天记录的频率作为每日前8小时销售量发生的概率，该生鲜超市当天销售有机蔬菜利润的期望值为决策依据，当购进17份比购进18份的利润的期望值大时，求的取值范围.
附：回归直线方程为
，其中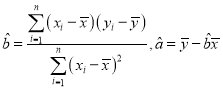
.
