题目内容
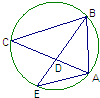 如图所示,圆的内接三角形ABC的角平分线BD与AC交于点D,与圆交于点E,连接AE,已知ED=3,BD=6,则线段AE的长=
如图所示,圆的内接三角形ABC的角平分线BD与AC交于点D,与圆交于点E,连接AE,已知ED=3,BD=6,则线段AE的长=分析:由已知中圆的内接三角形ABC的角平分线BD与AC交于点D,结合圆周角定理,我们可得△EDA和△EAB中,∠E=∠E,∠EAD=∠EBA,由相似三角形判定定理得△EDA∽△EAB,进而根据相似三角形性质,得到AE:BE=ED:AE,根据已知中ED=3,BD=6,即可求出线段AE的长.
解答:解:∵BD平分角∠CBA,
∴∠CBE=∠EBA
又∵∠CBE=∠EAD
在△EDA和△EAB中,
∠E=∠E,∠EAD=∠EBA
∴△EDA∽△EAB
∴AE:BE=ED:AE
∴AE2=ED•BE
又∵ED=3,BD=6,
∴BE=9
∴AE2=27
∴AE=3
故答案为:3
∴∠CBE=∠EBA
又∵∠CBE=∠EAD
在△EDA和△EAB中,
∠E=∠E,∠EAD=∠EBA
∴△EDA∽△EAB
∴AE:BE=ED:AE
∴AE2=ED•BE
又∵ED=3,BD=6,
∴BE=9
∴AE2=27
∴AE=3
| 3 |
故答案为:3
| 3 |
点评:本题考查的知识点是相似三角形的判定及性质,圆周角定理,其中根据BD平分角∠CBA,及圆周角定理,判断出△EDA∽△EAB是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
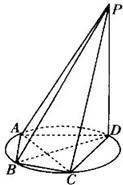 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
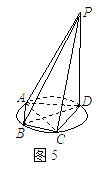
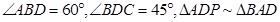 。
。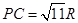 ,求三棱锥P—ABC的体积。
,求三棱锥P—ABC的体积。