题目内容
已知函数![]() (
(![]() )是偶函数且
)是偶函数且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间 ![]() 上的值域为
上的值域为![]() ? 若存在,求出
? 若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(满分10分)
(1)![]()
![]()
![]()
![]()
![]()
![]() 对于任意
对于任意![]() 恒成立
恒成立![]()
![]()
![]()
(2)由(1)得f(x)= x 2 , ∴ g (x) = 1-λ x2 + (2 λ-1) x
 又
又 ![]() ∴ g(x) =
∴ g(x) = ![]() =
=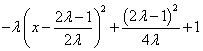
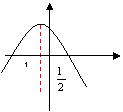
故 g(x) 的对称轴为 ![]()
|
|
方法一:
① ∵ x ∈[-1,2 ]
∴ 当 ![]() 即
即 ![]() 时,
时,
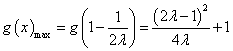 ;
;
![]() = -1
= -1![]()
![]() 不符合题意
不符合题意 ![]() 舍去
舍去
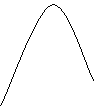 ② 当
② 当 ![]() 即 l ≥ 1时 ,
即 l ≥ 1时 ,
|
|
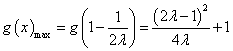
|
|
依题意得: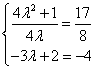 解得 :l = 2
解得 :l = 2
综上得:存在实数 l = 2 满足题意。
方法二:
∵对称轴 ![]() 且x ∈[-1,2 ] ,图像开口向下
且x ∈[-1,2 ] ,图像开口向下
∴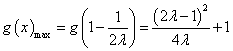
![]()
依题意 g(x)max = ![]() ∴
∴![]() =
= ![]()
解得:![]() (舍去) 或
(舍去) 或 ![]()
检验:当![]() 时,g(x)=
时,g(x)= ![]()
∵ x ∈[-1,2 ]
∴ x = ![]() 时,g(x)max =
时,g(x)max = ![]() , x = -1 时
, x = -1 时![]() = -4
= -4
符合题意。
综上得 :![]()

练习册系列答案
相关题目
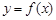 满足:①
满足:①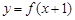 是偶函数;②在区间
是偶函数;②在区间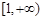 上是增函数.若
上是增函数.若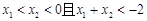 ,则
,则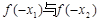 的大小关系是( )
的大小关系是( )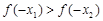 B.
B.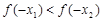 C.
C.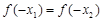 D.无法确定
D.无法确定 (
( )是偶函数
)是偶函数 的值;
的值; ,若函数
,若函数 与
与 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围
的取值范围 ,证明:
,证明: 是偶函数; (2)
是偶函数; (2) 上是增函数。
上是增函数。 >0恒成立,则下列不等式成立的是
>0恒成立,则下列不等式成立的是