题目内容
已知函数 的定义域为R,若存在常数
的定义域为R,若存在常数 ,对任意
,对任意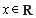 ,有
,有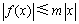 ,则称
,则称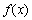
为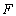 函数.给出下列函数:①
函数.给出下列函数:① ; ②
; ②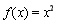 ; ③
; ③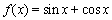 ;
;
④ ; ⑤
; ⑤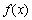 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数 均
均
有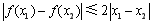 .其中是
.其中是 函数的序号为( )
函数的序号为( )
A.①②④ B.②③④ C.①④⑤ D.①②⑤
【答案】
C
【解析】
试题分析:由函数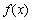 的定义域为R,若存在常数
的定义域为R,若存在常数 ,对任意
,对任意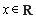 ,有
,有 ,则称
,则称
为 函数.因为
函数.因为 ,所存在m使得
,所存在m使得 恒成立,所以①正确.若
恒成立,所以①正确.若 成立,则
成立,则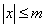 .显然不存在这样的m.所以②不正确. 若存在常数
.显然不存在这样的m.所以②不正确. 若存在常数 ,对任意
,对任意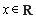 都有
都有 成立,当x=0时不成立.,所以③不正确.
成立,当x=0时不成立.,所以③不正确.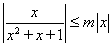 显然存在m,所以④正确. 若
显然存在m,所以④正确. 若 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数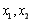 均
均
有 ,令
,令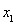 或
或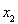 等于零时,即符合要求.综上所以①④⑤正确.故选C.
等于零时,即符合要求.综上所以①④⑤正确.故选C.
考点:1.新定义的问题.2.不等式恒成立问题.3.函数的最值.4.假命题的证明方法.5.特值法的思想.

练习册系列答案
相关题目
 的定义域为R,且当
的定义域为R,且当 时,
时, 恒成立,
恒成立, 对称;
对称; 图象的一个对称点。
图象的一个对称点。 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且
 N*),则
N*),则 的值为( )
的值为( ) 的定义域为R,它的反函数为
的定义域为R,它的反函数为 ,如果
,如果 与
与 互为反函数,且
互为反函数,且 ,则
,则 的值为(
)
的值为(
) B、0
C、
B、0
C、 D、
D、
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且 (
( N*),则
N*),则 的值为( )
的值为( )