题目内容
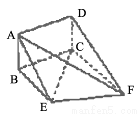
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为![]() ?
?
本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.
方法一:
(Ⅰ)证明:过点![]() 作
作![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,

可得四边形![]() 为矩形,
为矩形,
又![]() 为矩形,
为矩形,
所以![]() ,从而四边形
,从而四边形![]() 为平行四边形,
为平行四边形,
故![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() .
.
由平面![]() 平面
平面![]() ,
,![]() ,得
,得
![]() 平面
平面![]() ,
,
从而![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,因为
中,因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() ,
,
从而![]() .
.
于是![]() .
.
因为![]() ,
,
所以当![]() 为
为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
方法二:如图,以点![]() 为坐标原点,以
为坐标原点,以![]() 和
和![]() 分别作为
分别作为![]() 轴,
轴,![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.

设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
故![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,从而
,从而
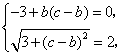
解得![]() .
.
所以![]() ,
,![]() .
.
设![]()
![]() 与平面
与平面![]() 垂直,
垂直,
则![]() ,
,
解得![]() .
.
又因为![]() 平面
平面![]() ,
,![]() ,
,
所以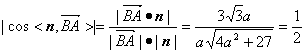 ,
,
得到![]() .
.
所以当![]() 为
为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 BCF=
BCF=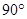 ,AD=
,AD=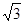 ,EF=2.
,EF=2. .
.
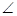 BCF=
BCF= ,AD=
,AD=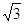 ,EF=2.
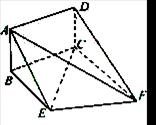
,EF=2.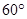 .
.
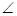 BCF=
BCF=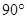 ,AD=
,AD=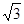 ,EF=2.
,EF=2.
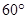 .
.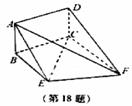 (Ⅰ)求证:AE//平面DCF;
(Ⅰ)求证:AE//平面DCF;