题目内容
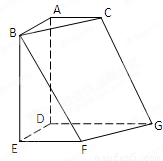
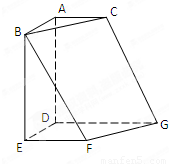
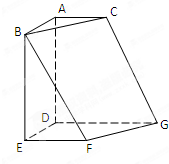 如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
(Ⅰ)求证:BF∥CG;
(Ⅱ)求三棱锥E-ABF的高.
(1)证明: 取DG的中点M,连接AM、FM
取DG的中点M,连接AM、FM
∵
∴EF∥DM,EF=DM
∴四边形EFMD为平行四边形
∴FM∥ED,FM=ED
∵四边形ABED为正方形
∴AB∥FM,AB=FM
∴四边形ABFM为平行四边形
∴AM∥BF
∵四边形ACGM为平行四边形
∴AM∥CG
∴BF∥CG
(2)设三棱锥E-ABF的高为h
∵正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,平面ABED∩平面ACGD=AD
AB⊥AD,GD⊥AD
∴AB⊥平面ACGD,GD⊥平面ABED
∴AB⊥AC,GD⊥平面ACED
∵EF∥AC
∴AB⊥EF,EF⊥平面ABED
 ∵AB⊥BE,BE?平面BEF,EF?平面BEF,EF∩BE=E
∵AB⊥BE,BE?平面BEF,EF?平面BEF,EF∩BE=E
∴AB⊥平面BEF,△ABF为直角三角形

由VE-ABF=VA-BEF得

∴
∴
∴h= .
.
故三棱锥E-ABF的高 .
.
分析:(Ⅰ)设M是DG的中点,由AC∥DG,且AC= ,得AC∥MG,AC=MG,四边形AMGC为平行四边形,得AM∥CG,同理可证四边形ABFM为平行四边形,得BF∥AM,AM∥CG,即可证得结论;
,得AC∥MG,AC=MG,四边形AMGC为平行四边形,得AM∥CG,同理可证四边形ABFM为平行四边形,得BF∥AM,AM∥CG,即可证得结论;
(Ⅱ)由VE-ABF=VA-BEF可求得三棱锥E-ABF的高为 .
.
点评:本题主要考查了利用公理4证明空间两条直线平行、棱锥高的计算.对于三棱锥高棱锥高的计算常常是利用等体积法.
 取DG的中点M,连接AM、FM
取DG的中点M,连接AM、FM∵

∴EF∥DM,EF=DM
∴四边形EFMD为平行四边形
∴FM∥ED,FM=ED
∵四边形ABED为正方形
∴AB∥FM,AB=FM
∴四边形ABFM为平行四边形
∴AM∥BF
∵四边形ACGM为平行四边形
∴AM∥CG
∴BF∥CG
(2)设三棱锥E-ABF的高为h
∵正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,平面ABED∩平面ACGD=AD
AB⊥AD,GD⊥AD
∴AB⊥平面ACGD,GD⊥平面ABED
∴AB⊥AC,GD⊥平面ACED
∵EF∥AC
∴AB⊥EF,EF⊥平面ABED
 ∵AB⊥BE,BE?平面BEF,EF?平面BEF,EF∩BE=E
∵AB⊥BE,BE?平面BEF,EF?平面BEF,EF∩BE=E∴AB⊥平面BEF,△ABF为直角三角形

由VE-ABF=VA-BEF得

∴

∴

∴h=
 .
.故三棱锥E-ABF的高
 .
.分析:(Ⅰ)设M是DG的中点,由AC∥DG,且AC=
 ,得AC∥MG,AC=MG,四边形AMGC为平行四边形,得AM∥CG,同理可证四边形ABFM为平行四边形,得BF∥AM,AM∥CG,即可证得结论;
,得AC∥MG,AC=MG,四边形AMGC为平行四边形,得AM∥CG,同理可证四边形ABFM为平行四边形,得BF∥AM,AM∥CG,即可证得结论;(Ⅱ)由VE-ABF=VA-BEF可求得三棱锥E-ABF的高为
 .
.点评:本题主要考查了利用公理4证明空间两条直线平行、棱锥高的计算.对于三棱锥高棱锥高的计算常常是利用等体积法.

练习册系列答案
相关题目
 如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.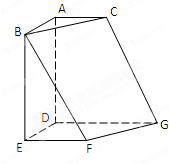 如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.
如图,正方形ABED、直角梯形EFGD、直角梯形ADGC所在平面两两垂直,AC∥DG∥EF.且DA=DE=DG=2,AC=EF=1.