题目内容
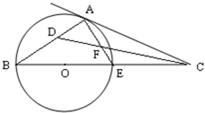
几何证明选讲如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.(1)求证:BA•DC=GC•AD;
(2)求BM.

【答案】分析:(1)根据AC⊥OB,及AD是圆O的直径,得到Rt△AGB和Rt△DCA相似,从而得到 ,又GC=AG,所以
,又GC=AG,所以 ,从而得到证明;
,从而得到证明;
(2)根据直角三角形中的边角关系求得BG,再根据直角三角形的相似及切割线定理求解即可.
解答:(1)证明:因为AC⊥OB,所以∠AGB=90°
又AD是圆O的直径,所以∠DCA=90°
又因为∠BAG=∠ADC(弦切角等于同弧所对圆周角)(3分)
所以Rt△AGB和Rt△DCA相似
所以
又因为OG⊥AC,所以GC=AG
所以 ,即BA•DC=GC•AD(5分)
,即BA•DC=GC•AD(5分)
(2)解:因为AC=12,所以AG=6,
因为AB=10,所以
由(1)知:Rt△AGB~Rt△DCA,.所以 (8分)
(8分)
所以AD=15,即圆的直径2r=15
又因为AB2=BM•(BM+2r),即BM2+15BM-100=0
解得BM=5(10分).
点评:本题考查的与圆有关的比例线段、圆周角及相似三角形的判定和性质,切割线定理的运用的综合运用.
 ,又GC=AG,所以
,又GC=AG,所以 ,从而得到证明;
,从而得到证明;(2)根据直角三角形中的边角关系求得BG,再根据直角三角形的相似及切割线定理求解即可.
解答:(1)证明:因为AC⊥OB,所以∠AGB=90°
又AD是圆O的直径,所以∠DCA=90°
又因为∠BAG=∠ADC(弦切角等于同弧所对圆周角)(3分)
所以Rt△AGB和Rt△DCA相似
所以

又因为OG⊥AC,所以GC=AG
所以
 ,即BA•DC=GC•AD(5分)
,即BA•DC=GC•AD(5分)(2)解:因为AC=12,所以AG=6,
因为AB=10,所以

由(1)知:Rt△AGB~Rt△DCA,.所以
 (8分)
(8分)所以AD=15,即圆的直径2r=15
又因为AB2=BM•(BM+2r),即BM2+15BM-100=0
解得BM=5(10分).
点评:本题考查的与圆有关的比例线段、圆周角及相似三角形的判定和性质,切割线定理的运用的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
 (2012•洛阳模拟)选修4-1:几何证明选讲
(2012•洛阳模拟)选修4-1:几何证明选讲 选修4-1:几何证明选讲
选修4-1:几何证明选讲