题目内容
设a、b、c分别是先后掷一枚质地均匀的正方体骰子三次得到的点数.
(1)求使函数f(x)=
bx3+
(a+c)x2+(a+c-b)x-4在R上不存在极值点的概率;
(2)设随机变量ξ=|a-b|,求ξ的分布列和数学期望.
(1)求使函数f(x)=
| 1 |
| 3 |
| 1 |
| 2 |
(2)设随机变量ξ=|a-b|,求ξ的分布列和数学期望.
分析:(1)由题意可得:若f(x)在R上不存在极值点,则f′(x)≥0恒成立,即△=(a+c-2b)2≤0,可得a、b、c成等差数列再结合a,b,c的取值计算出概率.
(2)随机变量ξ可能取的值为0,1,2,3,4,5,分别列出计算出其包含的基本事件,再求出其发生的概率,进而列出分布列求出期望.
(2)随机变量ξ可能取的值为0,1,2,3,4,5,分别列出计算出其包含的基本事件,再求出其发生的概率,进而列出分布列求出期望.
解答:解:(1)由题意可得:f′(x)=bx2+(a+c)x+(a+c-b)…(1分)
若f(x)在R上不存在极值点,则f′(x)≥0恒成立
∴△=(a+c)2-4b(a+c-b)≤0…(2分)即(a+c-2b)2≤0
∴a+c=2b
∴a、b、c成等差数列…(4分)
又a,b,c∈{1,2,3,4,5,6}
按公差分类a、b、c成等差数列共有6+4×2+4=18种情况
故函数f(x)在R上不存在极值点的概率P=
=
…(6分)
(2)随机变量ξ可能取的值为0,1,2,3,4,5
若ξ=0,则a=b,所以P(ξ=0)=
=
若ξ=1,则a=b+1或b=a+1,所以P(ξ=1)=
=
同理:P(ξ=2)=
=
,P(ξ=3)=
=
,P(ξ=4)=
=
,P(ξ=5)=
=
…(10分)
ξ的分布列为
所以Eξ=0×
+1×
+2×
+3×
+4×
+5×
=
…(13分)
若f(x)在R上不存在极值点,则f′(x)≥0恒成立
∴△=(a+c)2-4b(a+c-b)≤0…(2分)即(a+c-2b)2≤0
∴a+c=2b
∴a、b、c成等差数列…(4分)
又a,b,c∈{1,2,3,4,5,6}
按公差分类a、b、c成等差数列共有6+4×2+4=18种情况
故函数f(x)在R上不存在极值点的概率P=
| 18 |
| 6×6×6 |
| 1 |
| 12 |
(2)随机变量ξ可能取的值为0,1,2,3,4,5
若ξ=0,则a=b,所以P(ξ=0)=
| 6 |
| 36 |
| 1 |
| 6 |
若ξ=1,则a=b+1或b=a+1,所以P(ξ=1)=
| 10 |
| 36 |
| 5 |
| 18 |
同理:P(ξ=2)=
| 8 |
| 36 |
| 2 |
| 9 |
| 6 |
| 36 |
| 1 |
| 6 |
| 4 |
| 36 |
| 1 |
| 9 |
| 2 |
| 36 |
| 1 |
| 18 |
ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
| 1 |
| 6 |
| 5 |
| 18 |
| 2 |
| 9 |
| 1 |
| 6 |
| 1 |
| 9 |
| 1 |
| 18 |
| 35 |
| 18 |
点评:解决此类问题的关键是熟练掌握等可能事件的概率,以及掌握离散型型随机变量的分布列与期望求法,是一个综合题,本题是一个中档题,注意运算结果不要出错.

练习册系列答案
相关题目
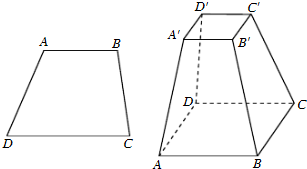 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.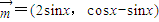 ,
,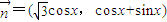 ,函数
,函数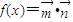 .
.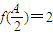 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.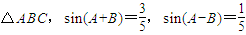 .
.

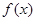 的最小正周期和值域;
的最小正周期和值域; 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状. .
. ;
; ,求AB边上的高CD的长.
,求AB边上的高CD的长.

 的最小正周期和值域;
的最小正周期和值域; 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状. .
. ;
; ,求AB边上的高CD的长.
,求AB边上的高CD的长.