题目内容
已知双曲线 的一条渐近线方程为
的一条渐近线方程为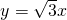 ,一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为
,一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为
- A.

- B.

- C.

- D.2
D
分析:写出双曲线的离心率,列出方程,求出a,b;利用离心率公式求出离心率.
解答: 的渐近线方程为
的渐近线方程为
∵一条渐近线方程为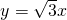
∴ ①
①
∵抛物线y2=8x的焦点为(2,0)
∴双曲线中的半焦距为c=2
∴a2+b2=4②
解①②得a=1,b=
所以双曲线的离心率为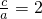
故选D
点评:解决双曲线的渐近线问题,要注意渐近线方程与双曲线的方程有关,只要将双曲线方程右边的1换为0即可.
分析:写出双曲线的离心率,列出方程,求出a,b;利用离心率公式求出离心率.
解答:
 的渐近线方程为
的渐近线方程为
∵一条渐近线方程为
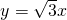
∴
 ①
①∵抛物线y2=8x的焦点为(2,0)
∴双曲线中的半焦距为c=2
∴a2+b2=4②
解①②得a=1,b=

所以双曲线的离心率为
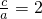
故选D
点评:解决双曲线的渐近线问题,要注意渐近线方程与双曲线的方程有关,只要将双曲线方程右边的1换为0即可.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线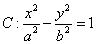
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
