题目内容
已知函数f(x)=x3+ax•2+bx+c,曲线y=f(x)在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
.若x=
时,y=f(x)有极值.
(1)求a、b、c的值;
(2)设g(x)=x3+k+8lnx,若关于x的方程f(x)=g(x)在[1,e]内有且只有一个实数根,求实数k的取值范围.
| ||
| 10 |
| 2 |
| 3 |
(1)求a、b、c的值;
(2)设g(x)=x3+k+8lnx,若关于x的方程f(x)=g(x)在[1,e]内有且只有一个实数根,求实数k的取值范围.
分析:(1)已知函数f(x)=x3+ax2+bx+c,对其进行求导,求出其在x=1处的斜率,求出其极值点,然后求出切线l的解析式,再根据点到直线的距离,切线l不过第四象限,得到m、a、b、c的值;
(2)由(1)可得f(x)=x3+2x2-4x+5,方程f(x)=g(x)可化为:2x2-4x-81nx+5=k,设h(x)=2x2-4x-8lnx+5(x>0),对其进行求导,得到其单调区间,从而求实数k的取值范围.
(2)由(1)可得f(x)=x3+2x2-4x+5,方程f(x)=g(x)可化为:2x2-4x-81nx+5=k,设h(x)=2x2-4x-8lnx+5(x>0),对其进行求导,得到其单调区间,从而求实数k的取值范围.
解答: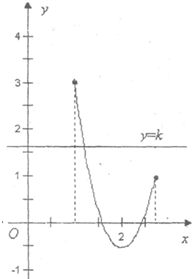 解:(1)由f(x)=x3+ax2+bx+c,得f'(x)=3x2+2ax+b.
解:(1)由f(x)=x3+ax2+bx+c,得f'(x)=3x2+2ax+b.
当x=1时,切线l的斜率为3,可得2a+b=0.…①
当x=
时,y=f(x)有极值,则f′(
)=0,可得4a+3b+4=0…②
由①、②解得a=2,b=-4.设切线l的方程为y=3x+m
由原点到切线l的距离为
,则
=
.
解得m=±1
∵切线l不过第四象限,
∴m=1,
∴切线方程为y=3x+1,
由于l切点的横坐标为x=1,
∴f(1)=4,
∴1+a+b+c=4,
∴c=5
∴a=2,b=-4,c=5
(2)由(1)可得f(x)=x3+2x2-4x+5,
方程f(x)=g(x)可化为:2x2-4x-81nx+5=k.
设h(x)=2x2-4x-8lnx+5(x>0),
则h′(x)=4x-
-4.
令h′(x)=0,得x=2(负值舍去).
∴h(x)在x=2处取得极小值h(2)=5-8ln2.
又h(1)=3,h(e)=2e2-4e-3,且h(e)<h(1).
∴h(x)的大致图象如右图:
∴由图知,当k=5-8ln2或2e2-4e-3<k≤3时,方程f(x)=g(x)在[1,e]内有且只有一个实数根.
 解:(1)由f(x)=x3+ax2+bx+c,得f'(x)=3x2+2ax+b.
解:(1)由f(x)=x3+ax2+bx+c,得f'(x)=3x2+2ax+b.当x=1时,切线l的斜率为3,可得2a+b=0.…①
当x=
| 2 |
| 3 |
| 2 |
| 3 |
由①、②解得a=2,b=-4.设切线l的方程为y=3x+m
由原点到切线l的距离为
| ||
| 10 |
| |m| | ||
|
| ||
| 10 |
解得m=±1
∵切线l不过第四象限,
∴m=1,
∴切线方程为y=3x+1,
由于l切点的横坐标为x=1,
∴f(1)=4,
∴1+a+b+c=4,
∴c=5
∴a=2,b=-4,c=5
(2)由(1)可得f(x)=x3+2x2-4x+5,
方程f(x)=g(x)可化为:2x2-4x-81nx+5=k.
设h(x)=2x2-4x-8lnx+5(x>0),
则h′(x)=4x-
| 8 |
| x |
令h′(x)=0,得x=2(负值舍去).
| x | [1,2) | 2 | (2,e] |
| h'(x) | - | O | + |
| h(x) | ↘ |
极小值 | ↗ |
又h(1)=3,h(e)=2e2-4e-3,且h(e)<h(1).
∴h(x)的大致图象如右图:
∴由图知,当k=5-8ln2或2e2-4e-3<k≤3时,方程f(x)=g(x)在[1,e]内有且只有一个实数根.
点评:此题主要考查导数研究区间的点的切线及其单调区间,还考查了点到直线的距离,有一定的难度,此题是一道综合题;

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|