题目内容
在平面直角坐标系中,若 ,且
,且 .
.
(1)求动点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点,设 ,是否存在这样的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程,不存在,说明理由.
,是否存在这样的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程,不存在,说明理由.
解:(1)因为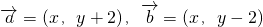 ,且
,且 .
.
所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8.
所以轨迹C以F1(0,-2),F2(0,2)为焦点的椭圆,
方程为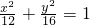 .
.
(2)为直线l过点(0,3).
若直线l是y轴,则A、B是椭圆的顶点.
 ,
,
所以O与P重合,与四边形OAPB是矩形矛盾.
所以直线l的斜率存在,
设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2)
由 ,
,
由于△=(18k2)-4(4+3k2)(-21)>0恒成立.
由韦达定理 .
.
因为 ,
,
所以OAPB是平行四边形.
若存在直线l,使得四边形OAPB为矩形,
则OA⊥OB,即 ,
,
因为 ,
, ,
,
所以 ,
,
所以(1+k2)x1x2+3k(x1+x2)+9=0,
所以
机 ,
,
故存在直线 ,使得四边形OAPB为矩形.
,使得四边形OAPB为矩形.
分析:(1)因为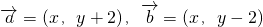 ,且
,且 .所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8.由此能求出动点M(x,y)的轨迹C的方程.
.所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8.由此能求出动点M(x,y)的轨迹C的方程.
(2)若直线l是y轴,则A、B是椭圆的顶点. ,所以O与P重合,与四边形OAPB是矩形矛盾.所以直线l的斜率存在,设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2),由
,所以O与P重合,与四边形OAPB是矩形矛盾.所以直线l的斜率存在,设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2),由 ,由于△=(18k2)-4(4+3k2)(-21)>0恒成立.由韦达定理
,由于△=(18k2)-4(4+3k2)(-21)>0恒成立.由韦达定理 .因为
.因为 ,所以OAPB是平行四边形.由此能够导出存在直线
,所以OAPB是平行四边形.由此能够导出存在直线 ,使得四边形OAPB为矩形.
,使得四边形OAPB为矩形.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.易错点是计算量大,容易出错.
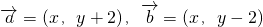 ,且
,且 .
.所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8.
所以轨迹C以F1(0,-2),F2(0,2)为焦点的椭圆,
方程为
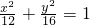 .
.(2)为直线l过点(0,3).
若直线l是y轴,则A、B是椭圆的顶点.
 ,
,所以O与P重合,与四边形OAPB是矩形矛盾.
所以直线l的斜率存在,
设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2)
由
 ,
,由于△=(18k2)-4(4+3k2)(-21)>0恒成立.
由韦达定理
 .
.因为
 ,
,所以OAPB是平行四边形.
若存在直线l,使得四边形OAPB为矩形,
则OA⊥OB,即
 ,
,因为
 ,
, ,
,所以
 ,
,所以(1+k2)x1x2+3k(x1+x2)+9=0,
所以

机
 ,
,故存在直线
 ,使得四边形OAPB为矩形.
,使得四边形OAPB为矩形.分析:(1)因为
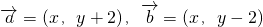 ,且
,且 .所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8.由此能求出动点M(x,y)的轨迹C的方程.
.所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8.由此能求出动点M(x,y)的轨迹C的方程.(2)若直线l是y轴,则A、B是椭圆的顶点.
 ,所以O与P重合,与四边形OAPB是矩形矛盾.所以直线l的斜率存在,设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2),由
,所以O与P重合,与四边形OAPB是矩形矛盾.所以直线l的斜率存在,设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2),由 ,由于△=(18k2)-4(4+3k2)(-21)>0恒成立.由韦达定理
,由于△=(18k2)-4(4+3k2)(-21)>0恒成立.由韦达定理 .因为
.因为 ,所以OAPB是平行四边形.由此能够导出存在直线
,所以OAPB是平行四边形.由此能够导出存在直线 ,使得四边形OAPB为矩形.
,使得四边形OAPB为矩形.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.易错点是计算量大,容易出错.

练习册系列答案
相关题目