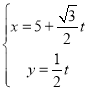题目内容
【题目】(本小题满分12分)如图,曲线![]() 由上半椭圆
由上半椭圆![]() 和部分抛物线
和部分抛物线![]()
![]() 连接而成,
连接而成, ![]() 的公共点为
的公共点为![]() ,其中
,其中![]() 的离心率为
的离心率为![]() .
.
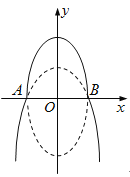
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 分别交于
分别交于![]() (均异于点
(均异于点![]() ),若
),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:(1)由上半椭圆![]() 和部分抛物
和部分抛物![]() 公共点为
公共点为![]() ,得
,得![]() ,设
,设![]() 的半焦距为
的半焦距为![]() ,由
,由![]() 及
及![]() ,解得
,解得![]() ;
;
(2)由(1)知,上半椭圆![]() 的方程为
的方程为![]() ,
, ![]() ,易知,直线
,易知,直线![]() 与
与![]() 轴不重合也不垂直,故可设其方程为
轴不重合也不垂直,故可设其方程为![]() ,并代入
,并代入![]() 的方程中,整理得:
的方程中,整理得: ![]() ,
,
由韦达定理得![]() ,又
,又![]() ,得
,得![]() ,从而求得
,从而求得![]() ,继而得点
,继而得点![]() 的坐标为
的坐标为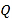 ,同理,由
,同理,由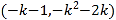 得点
得点![]() 的坐标为
的坐标为![]() ,最后由
,最后由![]() ,解得
,解得![]() ,经检验
,经检验![]() 符合题意,故直线
符合题意,故直线![]() 的方程为
的方程为![]() .
.
试题解析:(1)在![]() 方程中,令
方程中,令![]() ,得
,得![]()
在![]() 方程中,令
方程中,令![]() ,得
,得![]()
所以![]()
设![]() 的半焦距为
的半焦距为![]() ,由
,由![]() 及
及![]() ,解得
,解得![]()
所以![]() ,
, ![]()
(2)由(1)知,上半椭圆![]() 的方程为
的方程为![]() ,
, ![]()
易知,直线![]() 与
与![]() 轴不重合也不垂直,设其方程为
轴不重合也不垂直,设其方程为![]()
代入![]() 的方程中,整理得:
的方程中,整理得:
![]() (*)
(*)
设点![]() 的坐标
的坐标![]()
由韦达定理得![]()
又![]() ,得
,得![]() ,从而求得
,从而求得![]()
所以点![]() 的坐标为
的坐标为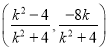
同理,由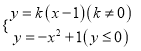 得点
得点![]() 的坐标为
的坐标为![]()
![]() ,
, ![]()
![]()
![]() ,即
,即![]()
![]() ,
, ![]() ,解得
,解得![]()
经检验, ![]() 符合题意,
符合题意,
故直线![]() 的方程为
的方程为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: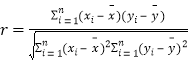 ,回归直线方程是
,回归直线方程是![]() ,
,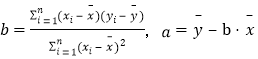 ,
,