题目内容
若sin(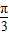 -a)=
-a)= ,则cos(
,则cos(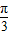 +2a)等于 .
+2a)等于 .
【答案】分析:将已知等式中的角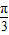 -α变形为
-α变形为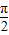 -(
-(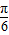 +α),利用诱导公式化简求出cos(
+α),利用诱导公式化简求出cos(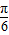 +α)的值,然后把所求式子利用二倍角的余弦函数公式化简后,将cos(
+α)的值,然后把所求式子利用二倍角的余弦函数公式化简后,将cos(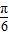 +α)的值代入即可求出值.
+α)的值代入即可求出值.
解答:解:∵sin(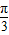 -α)=sin[
-α)=sin[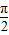 -(
-(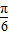 +α)]=cos(
+α)]=cos(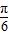 +α)=
+α)= ,
,
∴cos(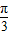 +2α)=cos2(
+2α)=cos2(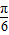 +α)=2cos2(
+α)=2cos2(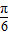 +α)-1=2×(
+α)-1=2×( )2-1=-
)2-1=- .
.
故答案为:-
点评:此题考查了二倍角的余弦函数公式,以及诱导公式,熟练掌握公式,灵活变换角度是解本题的关键.
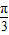 -α变形为
-α变形为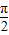 -(
-(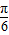 +α),利用诱导公式化简求出cos(
+α),利用诱导公式化简求出cos(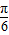 +α)的值,然后把所求式子利用二倍角的余弦函数公式化简后,将cos(
+α)的值,然后把所求式子利用二倍角的余弦函数公式化简后,将cos(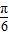 +α)的值代入即可求出值.
+α)的值代入即可求出值.解答:解:∵sin(
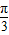 -α)=sin[
-α)=sin[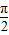 -(
-(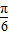 +α)]=cos(
+α)]=cos(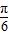 +α)=
+α)= ,
,∴cos(
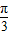 +2α)=cos2(
+2α)=cos2(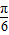 +α)=2cos2(
+α)=2cos2(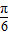 +α)-1=2×(
+α)-1=2×( )2-1=-
)2-1=- .
.故答案为:-

点评:此题考查了二倍角的余弦函数公式,以及诱导公式,熟练掌握公式,灵活变换角度是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若sin(π+A)=-
,则cos(
π-A)的值是( )
| 1 |
| 2 |
| 3 |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
在△ABC中,若sin(A+B-C)=sin(A-B+C),则△ABC必是( )
| A、等腰三角形 | B、直角三角形 | C、等腰或直角三角形 | D、等腰直角三角形 |