题目内容
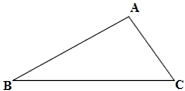 如图,在△ABC中,BC、CA、AB的长分别为a,b,c,
如图,在△ABC中,BC、CA、AB的长分别为a,b,c,
(1)求证:a=bcosC+ccosB;
(2)若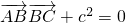 ,试证明△ABC为直角三角形.
,试证明△ABC为直角三角形.
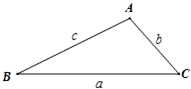 解:(1)∵
解:(1)∵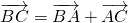 ,
,∴
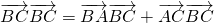
∴a2=accosB+bacosC
∴a=bcosC+ccosB
(2)由
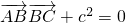 得
得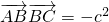 ,
,而
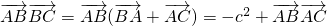
∴
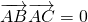 ,∴△ABC为直角三角形
,∴△ABC为直角三角形证法二:由(1)类似可证得:c=acosB+bcosA(*)
由
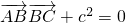 得,accos(π-B)+c2=0.即:c2=accosB
得,accos(π-B)+c2=0.即:c2=accosB∴c=acosB,结合(*)式得bcosA=0
∴A=90°,∴△ABC为直角三角形.
分析:(1)通过
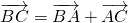 ,两边平方化简,即可证明a=bcosC+ccosB;
,两边平方化简,即可证明a=bcosC+ccosB;(2)利用
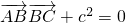 ,转化为
,转化为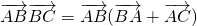 ,推出
,推出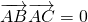 ,即可证明△ABC为直角三角形.
,即可证明△ABC为直角三角形.法二:利用(1)的结论,直接化简
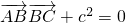 推出bcosA=0,说明A=90°即可.
推出bcosA=0,说明A=90°即可.点评:本题是中档题,通过向量的数量积转化为三角函数的有关知识,考查三角形的判定,计算能力常考题型,注意本题的解法比较多,(1)也可以取与
 同向的单位向量
同向的单位向量 ,在
,在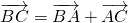 的两边作数量积,同样可证.
的两边作数量积,同样可证. 
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知