Question

（2013•莱芜二模）已知定点A(

p

2

，0)（p为常数，p＞O），B为x轴负半轴上的一个动点，动点M使得|AM|=|AB|，且线段BM的中点在y轴上．
（I）求动点M的轨迹C的方程；
（Ⅱ）设EF为曲线C的一条动弦（EF不垂直于x轴），其垂直平分线与x轴交于点T（4，0），当p=2时，求|EF|的最大值．

Answer 1

分析：（Ⅰ）设出动点M的坐标，由题意把B和G用M的坐标表示，根据|AM|=|AB|，可知GA⊥GM，写出对应的向量的坐标，由数量积等于0列式可得M的轨迹C的方程，注意M在x轴上时不合题意； 
（Ⅱ）设出EF所在直线方程y=kx+b，和抛物线方程联立后化为关于x的一元二次方程，利用根与系数关系求出EF中点的坐标，写出其垂直平分线方程，由垂直平分线过点T（4，0），得到k和b的关系，用k表示b，由方程的判别式大于0求出k的范围，由弦长公式写出EF的长度，最后利用配方法球最值．

解答：解：如图，

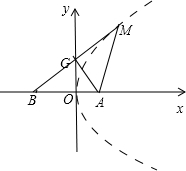
（Ⅰ）设M（x，y），则BM的中点G的坐标为(0，

y

2

)，B（-x，0）．
又A（

p

2

，0），故

GA

=(

p

2

，-

y

2

)，

GM

=(x，

y

2

)．
由题意知GA⊥GM，所以

GA

•

GM

=

px

2

-

y2

4

=0，
所以y²=2px．
当M点在x轴上时不满足题意，故曲线C的方程为y²=2px（p＞0，x≠0）；
（Ⅱ）设弦EF所在直线方程为y=kx+b，E（x₁，y₁），F（x₂，y₂）．
由

y=kx+b y2=4x

，得：k²x²+（2kb-4）x+b²=0①
则x1+x2=

4-2kb

k2

，x1x2=

b2

k2

．
则线段EF的中点为(

2-kb

k2

，

2-kb

k

+b)，即(

2-kb

k2

，

2

k

)．
线段EF的垂直平分线方程为y-

2

k

=-

1

k

(x-

2-kb

k2

)．
令y=0，x=4，得-

2

k

=-

1

k

(4-

2-kb

k2

)，得bk=2-k²，所以b=

2-k2

k

．
所以|EF|2=(1+k2)•(x1-x2)2=(1+k2)•[(x1+x2)2-4x1x2]
=(1+k2)[(

4-2kb

k2

)2-

4b2

k2

]=16(1+k2)•

1-kb

k4

=16(1+k2)•

2k2-1

k4

=16(-

1

k4

+

1

k2

+2)=-16(

1

k2

-

1

2

)2+36．
再由①，△=（2kb-4）²-4k²b²=4k²b²-16kb+16-4k²b²=16-16kb
=16-16（2-2k²）=32k²-16＞0．
得：k2＞

1

2

，即0＜

1

k2

＜2．
所以，当

1

k2

=

1

2

，即k=±

2

时，|EF|²取得最大值，最大值等于36，即|EF|的最大值为6．

点评：本题考查了抛物线的标准方程，考查了直线与圆锥曲线的关系，直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现，主要涉及位置关系的判定，弦长问题、轨迹问题等．突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法．属难题．