题目内容
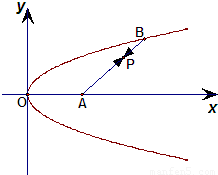
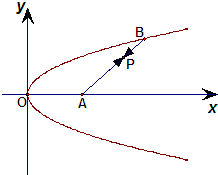如图，已知定点A（2，0）及抛物线y2=x，点B在该抛物线上，若动点P使得
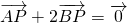，求动点P的轨迹方程．
解：设点P的坐标为（x，y），则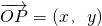
，
，
∵，
∴
，
∴
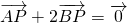，即点B坐标为
，
而点B在抛物线y2=x上，因此有：
，即
．
∴动点P的轨迹方程为．
分析：设动点的坐标为P（x，y），得到
，
的坐标表示，然后根据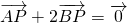得出
求出B点的坐标，进而代入抛物线方程即可得答案．
点评：本题主要考查通过向量的有关运算求轨迹方程的问题．对向量的有关题型比如：求模、求夹角、求垂直以及平行等的问题一定要强化练习，是高考的热点问题．
，，∵
，∴
，∴
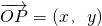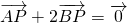，即点B坐标为，而点B在抛物线y2=x上，因此有：
，即．∴动点P的轨迹方程为
．分析：设动点的坐标为P（x，y），得到
，的坐标表示，然后根据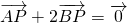得出求出B点的坐标，进而代入抛物线方程即可得答案．点评：本题主要考查通过向量的有关运算求轨迹方程的问题．对向量的有关题型比如：求模、求夹角、求垂直以及平行等的问题一定要强化练习，是高考的热点问题．
练习册系列答案
相关题目
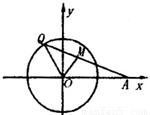
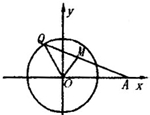如图，已知定点A（2，0），点Q是圆x2+y2=1上的动点，∠AOQ的平分线交AQ于M，当Q点在圆上移动时，求动点M的轨迹方程．
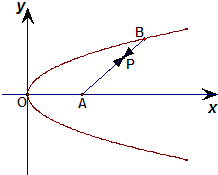如图，已知定点A（2，0）及抛物线y2=x，点B在该抛物线上，若动点P使得
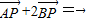，求动点P的轨迹方程．
