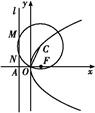
题目内容
设定圆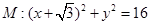 ,动圆
,动圆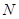 过点
过点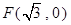 且与圆
且与圆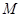 相切,记动圆
相切,记动圆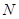 圆心
圆心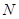 的轨迹为
的轨迹为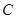 .
.
(1)求轨迹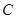 的方程;
的方程;
(2)已知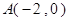 ,过定点
,过定点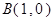 的动直线
的动直线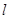 交轨迹
交轨迹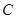 于
于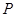 、
、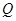 两点,
两点,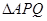 的外心为
的外心为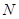 .若直线
.若直线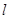 的斜率为
的斜率为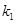 ,直线
,直线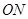 的斜率为
的斜率为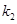 ,求证:
,求证: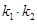 为定值.
为定值.
(1)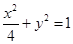 ;(2)见解析
;(2)见解析
解析试题分析:(1)求轨迹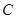 的方程,由题意定圆
的方程,由题意定圆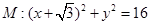 ,动圆
,动圆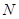 过点
过点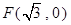 且与圆
且与圆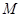 相切,可知点
相切,可知点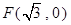 在圆
在圆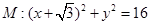 内,由此可得圆
内,由此可得圆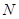 内切于圆
内切于圆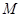 ,可得
,可得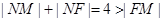 ,根据椭圆定义可知轨迹
,根据椭圆定义可知轨迹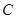 为椭圆,故可求出轨迹
为椭圆,故可求出轨迹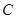 的方程;(2)求证:
的方程;(2)求证: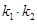 为定值,由题意直线
为定值,由题意直线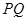 斜率不为0,可设直线
斜率不为0,可设直线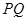 为
为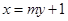 , 设点
, 设点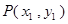 ,
,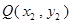 ,由
,由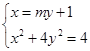
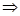
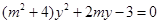 ,由根与系数关系得
,由根与系数关系得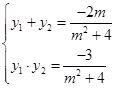 ,写出直线
,写出直线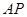 的中垂线方程,与直线
的中垂线方程,与直线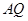 的中垂线方程,求出点
的中垂线方程,求出点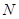 的坐标,即得直线
的坐标,即得直线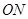 的斜率,从而可得
的斜率,从而可得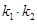 为定值.
为定值.
试题解析:(1)∵点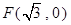 在圆
在圆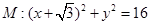 内 ∴圆
内 ∴圆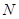 内切于圆
内切于圆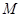
∴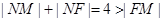
∴点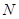 的轨迹
的轨迹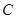 .的方程为
.的方程为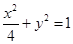 5分
5分
(2)由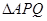 存在 ∴ 直线
存在 ∴ 直线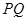 斜率不为0
斜率不为0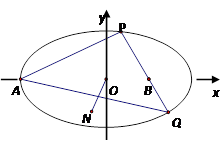
设直线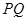 为
为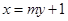 设点
设点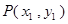 ,
,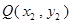
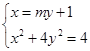
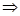
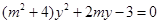
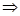
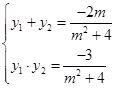
直线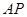 的中垂线方程为:
的中垂线方程为: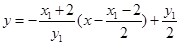
即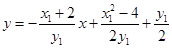 ∵
∵ ∴即
∴即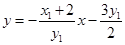
即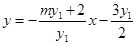 即
即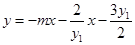
同理可得直线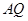 的中垂线方程为:
的中垂线方程为: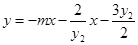 7分
7分
∴点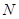 的坐标满足
的坐标满足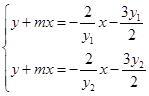
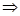

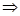
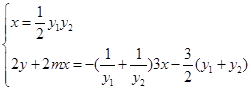
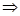
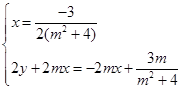 9分
9分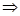
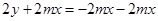
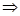

练习册系列答案
相关题目
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴的一个端点为M(0,1),直线l:y=kx-
,短轴的一个端点为M(0,1),直线l:y=kx-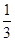 与椭圆相交于不同的两点A、B.
与椭圆相交于不同的两点A、B.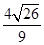 ,求k的值;
,求k的值;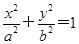 =1(a>b>0),点P
=1(a>b>0),点P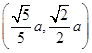 在椭圆上.
在椭圆上.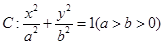 经过点
经过点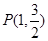 ,离心率
,离心率 ,直线
,直线 的方程为
的方程为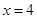 .
.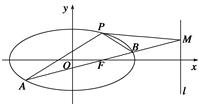
 的方程;
的方程;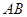 是经过右焦点
是经过右焦点 的任一弦(不经过点
的任一弦(不经过点 ),设直线
),设直线 ,记
,记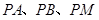 的斜率分别为
的斜率分别为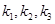 .问:是否存在常数
.问:是否存在常数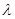 ,使得
,使得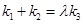 ?若存在,求
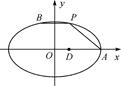
?若存在,求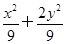 =1的右顶点,点D(1,0),点P、B在椭圆上,
=1的右顶点,点D(1,0),点P、B在椭圆上,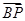 =
=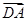 .
.
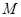 到两定点
到两定点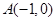 、
、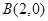 构成
构成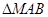 ,且
,且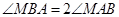 ,设动点
,设动点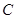 。
。
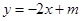 与
与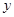 轴交于点
轴交于点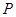 ,与轨迹
,与轨迹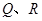 ,且
,且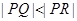 ,求
,求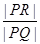 的取值范围。
的取值范围。 +
+ =1(a>b>0),抛物线C2:x2+by=b2.
=1(a>b>0),抛物线C2:x2+by=b2.
 ,
, b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,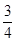 b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.