题目内容
已知圆锥曲线![]() 的焦点为
的焦点为![]() ,相应的准线方程为
,相应的准线方程为![]() ,且曲线
,且曲线![]() 过定点
过定点![]() .
.
又直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)试判断是否存在直线![]() ,使得点
,使得点![]() 是△
是△![]() 的重心.若存在,求出对应的直线
的重心.若存在,求出对应的直线![]() 的方程;
的方程;
若不存在,请说明理由;
(3)试判断是否存在直线![]() ,使得点
,使得点![]() 是△
是△![]() 的的垂心.若存在,求出对应的直线
的的垂心.若存在,求出对应的直线![]() 的方程;
的方程;
若不存在,请说明理由.
解:(1)根据圆锥曲线的第二定义知,曲线C的离心率根据圆锥曲线的第二定义知,
曲线C的离心率e=![]() <1,故为椭圆,
<1,故为椭圆,
根据条件解得曲线C的轨迹方程为:![]() . -----------------4分;
. -----------------4分;
(2)假设存在直线l,使得点F是△BMN的重心.
再设直线l与椭圆![]() .的交点M、N的坐标分别为M(x1,y1)、N(x2,y2),
.的交点M、N的坐标分别为M(x1,y1)、N(x2,y2),
则由椭圆几何性质的范围性知:-![]() ≤x1≤
≤x1≤![]() , -
, -![]() ≤x2≤
≤x2≤![]() ,则-2
,则-2![]() ≤x1+x2≤2
≤x1+x2≤2![]() <3,
<3,
另一方面,F(1,0)是△BMN的重心, 结合 B(0,1)及重心坐标公式知3×1=0+x1+x2,
即x1+x2=3,这与x1+x2≤2![]() <3矛盾, 故满足要求的直线l不存在. --------------8分;
<3矛盾, 故满足要求的直线l不存在. --------------8分;
(3)假设存在直线l,使得点F是△BMN的垂心. 由B(0,1)、F(1,0),知直线BF的斜率为-1. 于是,由BF⊥MN,知直线l的斜率为1. 设直线l方程为y=x+b. 与![]() 联立消去y,得3x2+4bx+2(b2-1)=0 (*)
联立消去y,得3x2+4bx+2(b2-1)=0 (*)
设M(x1,y1)、N(x2,y2),根据韦达定理得x1+x2=-![]() , x1x2=
, x1x2=![]() .
.
若再能保证NF⊥BM,即·=0,则F必为△BMN的垂心.
∵=(1-x2,-y2), =(x1,y1-1)
·=(1-x2)x1-y2(y1-1)=x1+y2-x1x2-y1y2=x1+(x2+b)-x1x2-(x1+b)(x2+b)
=-2x1x2+(1-b)(x1+x2)+b-b2=-2·![]() +b-b2=0
+b-b2=0
即3b2+b-4=0,解得b=1或b=-![]() .
.
当b=1时,点B即为直线l与椭圆的交点,不合题意;
当b=-![]() 时,代入方程(*)得3x2-
时,代入方程(*)得3x2-![]() x+
x+![]() =0,其判别式△=
=0,其判别式△=![]() =
=![]() >0,则两端点存在,
>0,则两端点存在,
满足题设.综上得,存在直线l: y=x-![]() ,使得点F是△BMN的垂心. ---------------------16分
,使得点F是△BMN的垂心. ---------------------16分

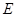 的两个焦点坐标是
的两个焦点坐标是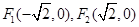 ,且离心率为
,且离心率为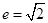 ;
;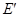 表示曲线
表示曲线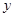 轴左边部分,若直线
轴左边部分,若直线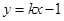 与曲线
与曲线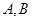 两点,求
两点,求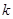 的取值范围;
的取值范围;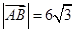 ,且曲线
,且曲线 ,使
,使 ,求
,求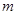 的值.
的值.
 为参数)和定点
为参数)和定点 ,
, 是此圆锥曲线的左、右焦点。
是此圆锥曲线的左、右焦点。 的极坐标方程;
的极坐标方程; ,且与直线
,且与直线 交此圆锥曲线于
交此圆锥曲线于 两点,求
两点,求 的值.
的值.